算法提升——栈和队列篇
最后更新时间:
基本原理
用底层链表结构
LinkedList实现栈结构1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19public class MyLinkedStack<E> {
// 直接调用底层 api
private MyLinkedList<E> list = new MyLinkedList<>();
// 压栈
public void push(E e) {
list.addLast(e);
}
// 弹栈
public E pop() {
return list.removeLast();
}
// 查看栈顶元素
public E peek() {
return list.getLast();
}
}构建双端队列
Deque底层使用数组的实现,如何高效使用?⇒ 环形数组
通过新增两个索引指针
first和last;注意last指针指向最后一个元素的后边,first指针指向第一个元素,即左闭右开区间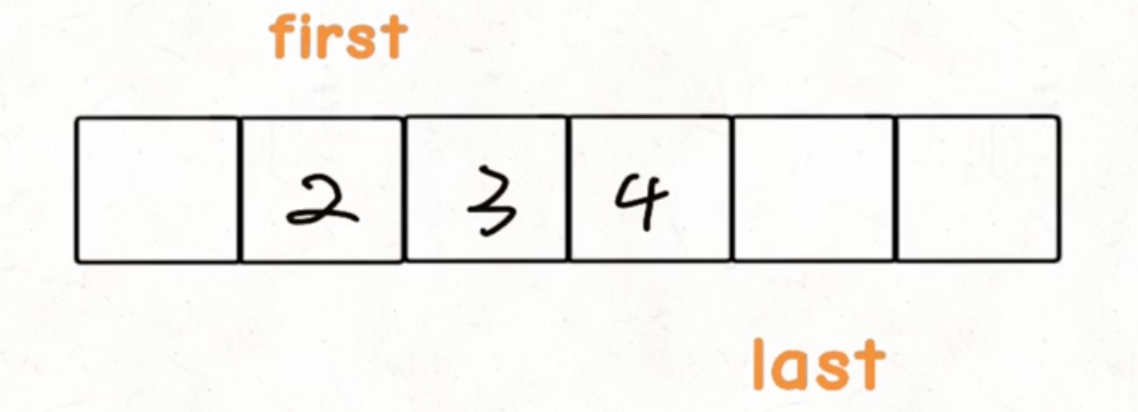
我们可以将其看作环,当
first指针在第一个元素时想要扩容,可以跳至尾部继续添加元素;直至first和last指向一样且数组中元素已满时再扩容1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102private void resize(int newCap) {
E[] temp = (E[]) new Object[newCap];
for (int i = 0; i < size; i++) {
temp[i] = data[(first + i) % data.length];
}
first = 0;
last = size;
data = temp;
}
public void addFirst(E e) {
// 扩容
if (size == data.length) {
resize(2 * data.length);
}
if (first == 0) {
first = data.length - 1;
} else {
first--;
}
// 插入数据
data[first] = e;
size++;
}
public void addLast(E e) {
if (size == data.length) {
resize(2 * data.length);
}
data[last] = e;
last++;
if (last == data.length) {
last = 0;
}
size++;
}
public E removeFirst() {
if (isEmpty()) {
throw new NoSuchElementException();
}
// 缩容
if (size == data.length / 4) {
resize(data.length / 2);
}
E oldVal = data[first];
data[first] = null;
first++;
if (first == data.length) {
first = 0;
}
size--;
return oldVal;
}
public E removeLast() {
if (isEmpty()) {
throw new NoSuchElementException();
}
// 缩容
if (size == data.length / 4) {
resize(data.length / 2);
}
if (last == 0) {
last = data.length - 1;
} else {
last--;
}
E oldVal = data[last];
data[last] = null;
size--;
return oldVal;
}
public E getFirst() {
if (isEmpty()) {
throw new NoSuchElementException();
}
return data[first];
}
public E getLast() {
if (isEmpty()) {
throw new NoSuchElementException();
}
if (last == 0) {
return data[data.length - 1];
}
return data[last - 1];
}RingBuffer结构API
1
2
3
4// 从 RingBuffer 中读取元素到 out 中,返回读取的字节数
public int read(byte[] out);
// 将 in 中的数据写入 RingBuffer, 返回写入的字节个数
public int write(byte[] in);工作原理
r 和 w 指针就类似前面提到的
first和last指针read 方法实际就是
removeFirst()write 方法实际就是
addLast()buffer 数组维护的实际就是一个先进先出的队列
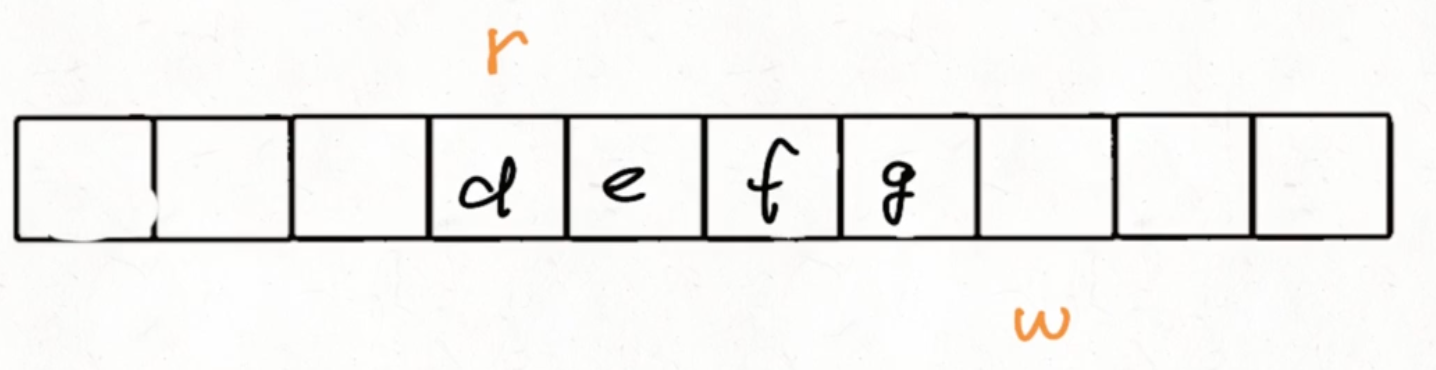
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118public RingBuffer(int cap) {
// 输入的 cap 变成 2 的指数
cap = ceilToPowerOfTwo(cap);
// (i + n) % capacity <=> (i + n) & mask
mask = cap - 1;
buffer = new byte[cap];
r = w = 0;
size = 0;
}
private static int ceilToPowerOfTwo(int n) {
if (n < 0) {
n = 2;
}
if (n > (1 << 30)) {
n = 1 << 30;
}
n--;
n |= n >> 1;
n |= n >> 2;
n |= n >> 4;
n |= n >> 8;
n |= n >> 16;
n++;
return n;
}
private void resize(int newCap) {
newCap = ceilToPowerOfTwo(newCap);
byte[] temp = new byte[newCap];
// 将 data 中的数据读入
int n = read(temp);
this.buffer = temp;
this.r = 0;
// 指向下一个元素
this.w = n;
this.mask = newCap - 1;
}
public int write(byte[] in) {
if (in == null || in.length == 0) {
return 0;
}
final int n = in.length;
// 还有多少空间
int free = buffer.length - size;
if (n > free) {
// 扩容
resize(size + n);
}
// 1. r ----- w
if (w >= r) {
if (w + n <= buffer.length){
// 1.1 r --- **w
System.arraycopy(in, 0, buffer, w, n);
} else {
// 1.2 **w r--**
int n1 = buffer.length - w;
int n2 = n - n1;
System.arraycopy(in, 0, buffer, w, n1);
System.arraycopy(in, 0, buffer, 0, n2);
}
} else {
// 2. --w r --
// buffer 空间足够,可直接写入
System.arraycopy(in, 0, buffer, w, n);
}
// w 指针前移
w = (w + n) & mask;
// 可读的增加了 n 个字节
size += n;
return n;
}
}
public int read(byte[] out) {
if (out == null || out.length == 0 || isEmpty()) {
return 0;
}
int n = Math.min(size, out.length);
// 1. r ----- w
if (r < w) {
// ***r--w
System.arraycopy(buffer, r, out, 0, n);
r += n;
size -= n;
return n;
}
// 2 --w r --
if (r + n <= buffer.length) {
// 2.1 --w **r--
System.arraycopy(buffer, r, out, 0, n);
} else {
// 2.2 **r--w ***
int n1 = buffer.length - r;
int n2 = n - n1;
System.arraycopy(buffer, r, out, 0, n1);
System.arraycopy(buffer, 0, out, n1, n2);
}
// r 前移
r = (r+n) & mask;
size -= n;
return n;
}PS: mask 使用技巧
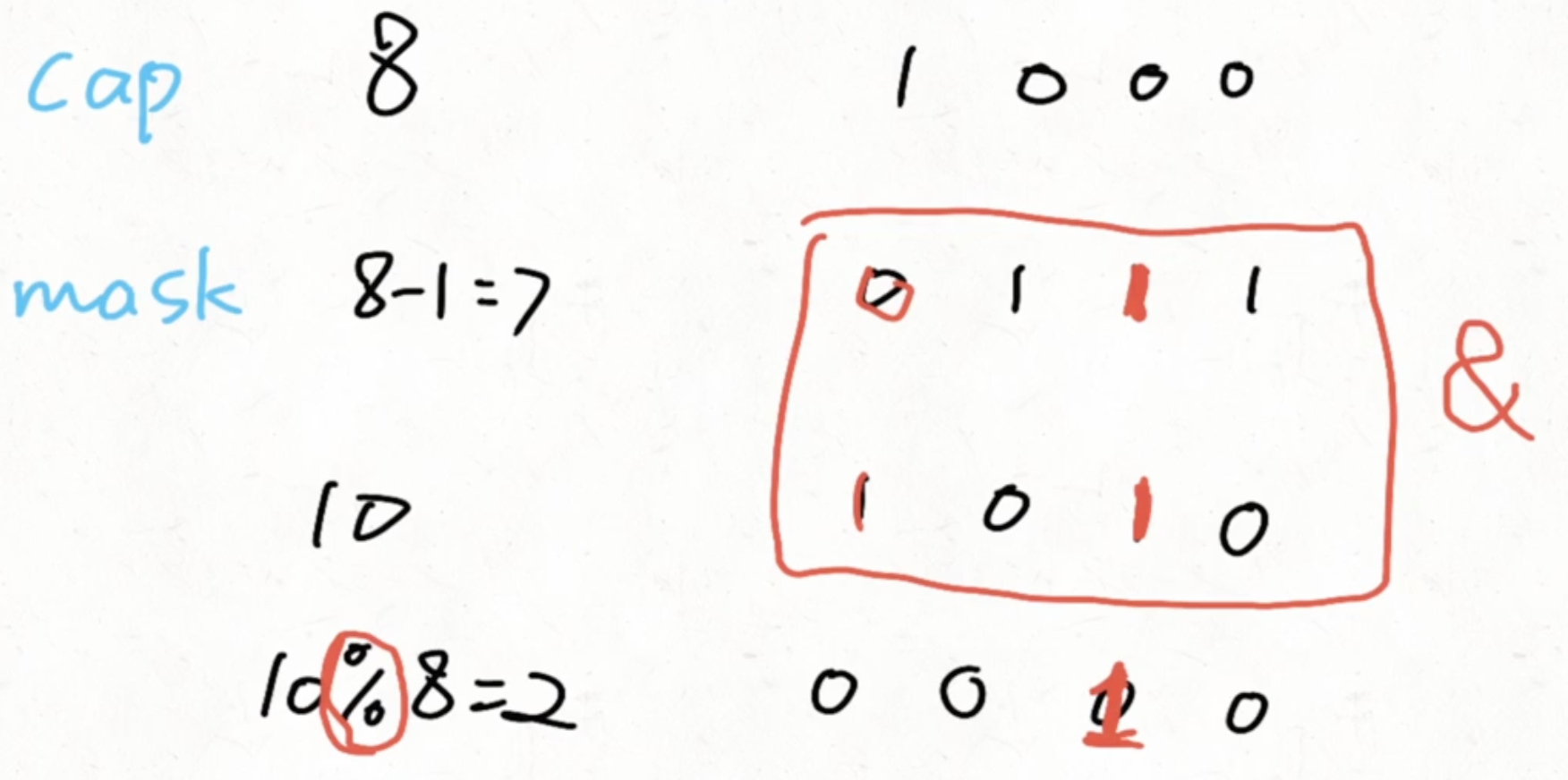
栈的经典习题
-
这道题目的是重构链表使之变成首尾交替链接,栈的结构就是可以构成一个逆序的链表节点。这里的难点在于处理最后节点,避免出现环路的情况。需要特别判断
next指针和temp指针的指向关系1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24public void reorderList(ListNode head) {
// 维护一个栈结构
Stack<ListNode> stack = new Stack<>();
ListNode p = head;
while (p != null) {
stack.push(p);
p = p.next;
}
p = head;
while (p != null) {
ListNode temp = stack.pop();
ListNode next = p.next;
// 考虑终止条件 => 分别对于偶数和奇数节点的情况
if (next == temp || temp.next == next) {
temp.next = null;
break;
}
p.next = temp;
temp.next = next;
//
p = next;
}
} -
这个就是最基本的栈匹配问题,考虑一下栈中只有一个元素的特殊情况即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30class Solution {
public boolean isValid(String s) {
Stack<Character> stack = new Stack<>();
for (char c : s.toCharArray()) {
if (c == '{' || c == '[' || c == '(') {
stack.push(c);
} else {
if (!stack.isEmpty() && getPair(stack.peek()) == c) {
stack.pop();
} else {
return false;
}
}
}
return stack.isEmpty() ? true : false;
}
private char getPair(char c) {
if (c == '{') {
return '}';
} else if (c == '[') {
return ']';
} else if (c == '(') {
return ')';
}
return '1';
}
} -
就是后缀表达式求值,编译原理课上也讲过具体的计算方法。通过维护一个栈,遇见操作数就弹栈并计算求和再压栈;遇见立即数就压栈
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25public int evalRPN(String[] tokens) {
Stack<Integer> stack = new Stack<>();
for (String token : tokens) {
if ("+-*/".contains(token)) {
// 注意立即数的顺序
int num1 = stack.pop();
int num2 = stack.pop();
switch (token) {
case "+": stack.push(num1 + num2);
break;
case "-": stack.push(num2 - num1);
break;
case "*": stack.push(num2 * num1);
break;
case "/": stack.push(num2 / num1);
break;
}
} else {
stack.push(Integer.parseInt(token));
}
}
return stack.pop();
} -
Java 提供了 Queue 接口可以作为底层数据结构,我们可以用 LinkedList 作为其实现类。即然要保证先入后出,那么我们每次就要记录栈顶的值,即队尾的值。在弹栈时,不停的出队直至栈顶元素在队列的队头为止。注意如果栈中元素超过1个时,我们还要记录下一个栈顶元素,因此在出队时还需要标记当前栈顶元素的前一个元素,方便下一次弹栈操作。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37class MyStack {
private Queue<Integer> queue;
// 记录队尾元素,下一次弹栈用
private int tail = 0;
public MyStack() {
queue = new LinkedList<>();
}
public void push(int x) {
queue.offer(x);
tail = x;
}
public int pop() {
int size = queue.size();
while (size > 2) {
queue.offer(queue.poll());
size--;
}
// 下一次的栈顶
tail = queue.peek();
queue.offer(queue.poll());
return queue.poll();
}
public int top() {
return tail;
}
public boolean empty() {
return queue.isEmpty();
}
} -
这题采取「空间换时间」策略,即维护另一栈用于存储对于当前栈顶元素而言到栈底的最小值,只需要在每次压栈的时候判断一下和当前最小栈栈顶元素大小关系即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34class MinStack {
private Stack<Integer> stack;
private Stack<Integer> miniStack;
public MinStack() {
stack = new Stack<>();
miniStack = new Stack<>();
}
public void push(int val) {
stack.push(val);
if (miniStack.isEmpty() || val <= miniStack.peek()) {
// 当前元素较小
miniStack.push(val);
} else {
// 最小栈中元素最小
miniStack.push(miniStack.peek());
}
}
public void pop() {
stack.pop();
miniStack.pop();
}
public int top() {
return stack.peek();
}
public int getMin() {
return miniStack.peek();
}
}
-
队列的经典习题
-
这里有个要求就是只记录最近 300s 的敲击次数,那么在返回值时如果队头元素时间戳超过了 300s 就直接出队忽略
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class HitCounter {
private Queue<Integer> queue;
public HitCounter() {
queue = new LinkedList<>();
}
public void hit(int timestamp) {
queue.offer(timestamp);
}
public int getHits(int timestamp) {
while (!queue.isEmpty() && timestamp - queue.peek() >= 300) {
// 仅记录最近 300s 的
queue.poll();
}
return queue.size();
}
} -
和上面这道题思想一样
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class RecentCounter {
private Queue<Integer> queque;
public RecentCounter() {
queque = new LinkedList<>();
}
public int ping(int t) {
while (!queque.isEmpty() && t - queque.peek() > 3000) {
queque.poll();
}
queque.offer(t);
return queque.size();
}
} -
这题刚开始写的很复杂,计算平均值都是先把多余的出队,实际上只用判断是否等于指定 size 就行,因为每次只会添加一个元素,所以如果超过了就出队一个。然后同时在已维护的队列元素总和上减去出队的元素值即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class MovingAverage {
private Queue<Integer> queue;
private int size;
private int queueSum = 0;
public MovingAverage(int size) {
queue = new LinkedList<>();
this.size = size;
}
public double next(int val) {
if (this.size == queue.size()) {
int del = queue.poll();
queueSum -= del;
}
queue.offer(val);
queueSum += val;
return queueSum * (1.0) / queue.size();
}
} -
这里采用数组作底层结构,注意 head 和 tail 的临界条件即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65class MyCircularQueue {
private int[] data;
private int size;
private int head;
private int tail;
public MyCircularQueue(int k) {
data = new int[k];
size = 0;
head = tail = 0;
}
public boolean enQueue(int value) {
if (isFull()) {
return false;
}
if (tail == data.length) {
tail = 0;
data[tail] = value;
}
data[tail] = value;
tail++;
size++;
return true;
}
public boolean deQueue() {
if (isEmpty()) {
return false;
}
data[head] = 0;
if (head == data.length - 1) {
head = 0;
} else {
head++;
}
size--;
return true;
}
public int Front() {
return isEmpty() ? -1 : data[head];
}
public int Rear() {
if (isEmpty()) {
return -1;
}
if (tail == 0) {
return data[data.length - 1];
}
return data[tail - 1];
}
public boolean isEmpty() {
return size == 0;
}
public boolean isFull() {
return size == data.length;
}
} -
跟循环队列差不多
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91class MyCircularDeque {
private int[] data;
private int size;
private int head;
private int tail;
public MyCircularDeque(int k) {
data = new int[k];
size = 0;
head = tail = 0;
}
public boolean insertFront(int value) {
if (isFull()) {
return false;
}
if (head == 0) {
head = data.length - 1;
} else {
head--;
}
data[head] = value;
size++;
return true;
}
public boolean insertLast(int value) {
if (isFull()) {
return false;
}
if (tail == data.length) {
tail = 0;
}
data[tail] = value;
tail++;
size++;
return true;
}
public boolean deleteFront() {
if (isEmpty()) {
return false;
}
data[head] = 0;
if (head == data.length - 1) {
head = 0;
} else {
head++;
}
size--;
return true;
}
public boolean deleteLast() {
if (isEmpty()) {
return false;
}
if (tail == 0) {
tail = data.length;
}
data[tail- 1] = 0;
tail--;
size--;
return true;
}
public int getFront() {
return isEmpty() ? -1 : data[head];
}
public int getRear() {
if (isEmpty()) {
return -1;
}
if (tail == 0) {
return data[data.length - 1];
}
return data[tail - 1];
}
public boolean isEmpty() {
return size == 0;
}
public boolean isFull() {
return size == data.length;
}
} -
这道题的难点在于从中间入队和出队,因此一个解决办法是将队列拆成两个左右列表。他们需要满足下列性质:
1、如果有偶数个元素时,
pushMiddle优先向右边添加2、如果有奇数个元素时,
popMiddle优先从右边删除3、如果只有 1 个元素,
popFront的时候,要去右边删除这个可以通过例子推断出来,每次都保证右边列表最多比左列表多一个元素。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87class FrontMiddleBackQueue {
private LinkedList<Integer> left;
private LinkedList<Integer> right;
public FrontMiddleBackQueue() {
left = new LinkedList<>();
right = new LinkedList<>();
}
private void balance() {
// 维护左列表和右列表的性质
// 右边只能比左边多一个
if (right.size() > left.size() + 1) {
left.addLast(right.removeFirst());
} else if (right.size() < left.size()) {
right.addFirst(left.removeLast());
}
}
public void pushFront(int val) {
left.addFirst(val);
balance();
}
public void pushMiddle(int val) {
if (size() % 2 == 0) {
// 偶数个元素往右列表插入
right.addFirst(val);
} else {
left.addLast(val);
}
balance();
}
public void pushBack(int val) {
right.addLast(val);
balance();
}
public int popFront() {
if (size() == 0) {
return -1;
}
int e;
// 只有一个元素时,只会在右列表里
if (size() == 1) {
e = right.removeLast();
} else {
e = left.removeFirst();
}
balance();
return e;
}
public int popMiddle() {
if (size() == 0) {
return -1;
}
int e;
if (size() % 2 == 0) {
// 偶数个元素从左列表移除
e = left.removeLast();
} else {
e = right.removeFirst();
}
balance();
return e;
}
public int popBack() {
if (size() == 0) {
return -1;
}
int e = right.removeLast();
balance();
return e;
}
private int size() {
return left.size() + right.size();
}
}
-
单调栈 ‼️
特性:每次新元素入栈后,栈内的元素都保持有序
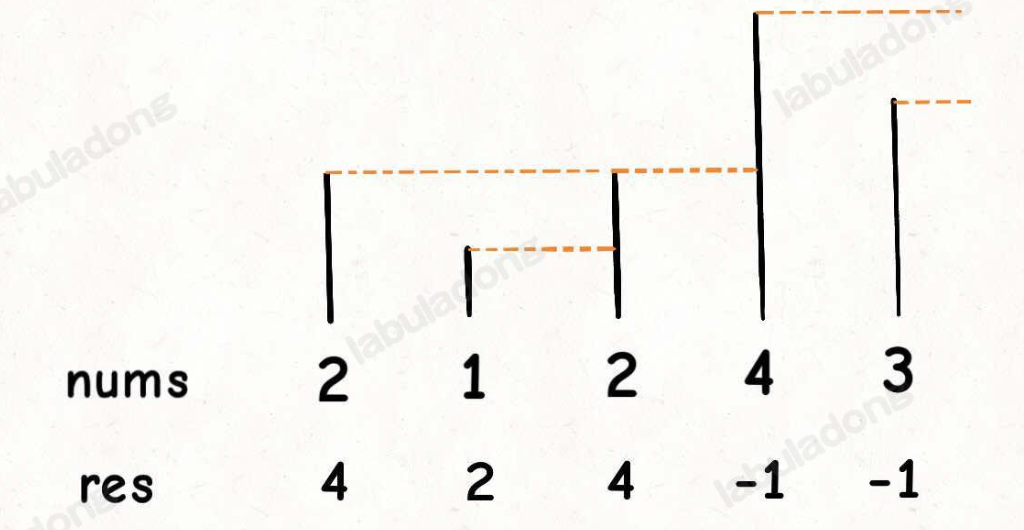
将其想象成比较身高大小,其第一个看见的露出头的元素即为符合要求的元素,因为后面的都被挡住了,结合栈结构,就是从后往前依次比较。由于栈 FILO 特性,每次得到的一定是最近的比它高的元素
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18int[] nextGreaterElement(int[] nums) {
int n = nums.length;
// 存放答案的数组
int[] res = new int[n];
Stack<Integer> s = new Stack<>();
// 倒着往栈里放
for (int i = n - 1; i >= 0; i--) {
// 判定个子高矮
while (!s.isEmpty() && s.peek() <= nums[i]) {
// 矮个起开,反正也被挡着了。。。
s.pop();
}
// nums[i] 身后的更大元素
res[i] = s.isEmpty() ? -1 : s.peek();
s.push(nums[i]);
}
return res;
}-
这道题由于 nums1 是 nums2 的子集,因此只需要先求出 nums2 元素的下一个更大元素结果,然后再由 nums1 去查找即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22public int[] nextGreaterElement(int[] nums1, int[] nums2) {
int n = nums2.length;
HashMap<Integer, Integer> map = new HashMap<>();
Stack<Integer> stack = new Stack<>();
for (int i = n - 1; i >= 0; i--) {
while (!stack.isEmpty() && stack.peek() <= nums2[i]) {
stack.pop();
}
int res = stack.isEmpty() ? -1 : stack.peek();
map.put(nums2[i], res);
stack.push(nums2[i]);
}
int[] res = new int[nums1.length];
for (int i = 0; i < nums1.length; i++) {
res[i] = map.get(nums1[i]);
}
return res;
} -
这题思路没转过来,单调栈里只要保存索引值即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16public int[] dailyTemperatures(int[] temperatures) {
Stack<Integer> stack = new Stack<>();
int[] res = new int[temperatures.length];
for (int i = temperatures.length - 1; i >= 0; i--) {
while (!stack.isEmpty() && temperatures[stack.peek()] <= temperatures[i]) {
stack.pop();
}
res[i] = stack.isEmpty() ? 0 : stack.peek() - i;
stack.push(i);
}
return res;
} 环形数组的解决
环形数组的特点在于其最后一个元素会紧接着第一个元素,解决这个问题实际是需要将数组长度翻倍即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17public int[] nextGreaterElements(int[] nums) {
int n = nums.length;
Stack<Integer> stack = new Stack<>();
int[] res = new int[n];
// 模拟翻倍,取模运算即可
for (int i = 2 * n - 1; i >= 0; i--) {
while (!stack.isEmpty() && stack.peek() <= nums[i % n]) {
stack.pop();
}
res[i % n] = stack.isEmpty() ? -1 : stack.peek();
stack.push(nums[i % n]);
}
return res;
}
-
单调栈变体 ‼️
下一个更大或相等的元素
把上面这段代码中 while 循环的
<=号改成<号即可下一个更小元素
while 循环的
<=条件改成>=条件即可下一个更小或相等元素
while 循环的
>=条件改成>即可上一个更大元素
从头至尾开始往栈里放元素即可,栈顶元素就是
nums[i]之前的元素上一个更大或相等的元素
同1
上一个更小的元素
同2
上一个更小或相等的元素
同3
-
只需要将链表先转换为数组即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21public int[] nextLargerNodes(ListNode head) {
ArrayList<Integer> arr = new ArrayList<>();
for (ListNode p = head; p != null; p = p.next) {
arr.add(p.val);
}
int n = arr.size();
int[] res = new int[n];
Stack<Integer> stack = new Stack<>();
for (int i = n - 1; i >= 0; i--) {
while (!stack.isEmpty() && stack.peek() <= arr.get(i))
{
stack.pop();
}
res[i] = stack.isEmpty() ? 0 : stack.peek();
stack.push(arr.get(i));
}
return res;
} -
这道题可以转为为求下一个更大或等于元素问题,只不过在统计的时候记录小于该元素身高的个数;另外一直困惑对于这种身高确实低于它的元素但是由于左边有比他高的所以不算是怎么解决的,应该是单调栈的特性,其中会保持单调递增特性(对于求下一更大元素而言),因此这个元素在之前计算时早就被弹栈出去了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21public int[] canSeePersonsCount(int[] heights) {
int n = heights.length;
// {身高,小于等于该身高人数}
int[] res = new int[n];
Stack<Integer> stack = new Stack<>();
for (int i = n - 1; i >= 0; i--) {
int count = 0;
while (!stack.isEmpty() && stack.peek() < heights[i]) {
stack.pop();
count++;
// 栈中元素单调递增 栈顶 -> 栈底
}
res[i] = stack.isEmpty() ? count : count + 1;
stack.push(heights[i]);
}
return res;
} -
经典单调栈下一个更小或相等元素问题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24public int[] finalPrices(int[] prices) {
int n = prices.length;
int[] res = new int[n];
Stack<Integer> stack = new Stack<>();
for (int i = n - 1; i >= 0; i--) {
while (!stack.isEmpty() && stack.peek() > prices[i]) {
stack.pop();
}
res[i] = stack.isEmpty() ? -1 : stack.peek();
stack.push(prices[i]);
}
for (int i = 0; i < n; i++) {
if (res[i] != -1) {
res[i] = prices[i] - res[i];
} else {
res[i] = prices[i];
}
}
return res;
} -
这道题转换一下思路,股票价格小于或等于今天价格的最大连续日数即向前看更大元素问题。但是这里注意要保留弹栈元素对应的大于价格天数的记录,这个源于单调栈的单调特性(这里是单调递减)
比如已经入栈的价格序列是
[40, 30, 20, 10],那么如果执行next(25),价格序列变成[40, 30, 25],20 和 10 都会被「挤掉」,算上 25 本身,函数返回 2 + 1 = 3。但还有个问题,这个 3 应该作为「权重」和 25 一同存储在栈中。因为之后 25 还可能被挤掉,比如说执行
next(26),价格序列就变成了[40, 30, 26],但这种情况下之前的 20 和 10 显然也应该被挤掉,函数应该返回 3 + 1 = 41
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class StockSpanner {
private Stack<int[]> stack;
public StockSpanner() {
stack = new Stack<>();
}
public int next(int price) {
// 算上当天
int count = 1;
while (!stack.isEmpty() && stack.peek()[0] <= price) {
// 保留每个价格的权值,即已经大于或等于的价格累计天数
count += stack.pop()[1];
}
stack.push(new int[]{price, count});
return count;
}
} -
这题需要保证修改后的数字最小,需要经过两步操作:
- k > 0 的情况下移除元素使得字符串中数字升序排布,可转化为向前看更大元素问题,保证单调栈中元素为升序
k > 0 的情况下移除字符串尾部元素,因为尾部元素最大
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33public String removeKdigits(String num, int k) {
Stack<Character> stack = new Stack<>();
for (char c : num.toCharArray()) {
// 保证单调栈是单增的
while (!stack.isEmpty() && stack.peek() > c && k > 0) {
stack.pop();
k--;
}
// 字符串不以 0 开头
if (stack.isEmpty() && c == '0') {
continue;
}
stack.push(c);
}
// 弹掉末尾的元素
while (k > 0 && !stack.isEmpty()) {
stack.pop();
k--;
}
if (stack.isEmpty()) {
return "0";
}
StringBuilder sb = new StringBuilder();
while (!stack.isEmpty()) {
sb.append(stack.pop());
}
// 出栈是以逆序字符串形式
return sb.reverse().toString();
}
单调队列
即满足队列中的元素都是单调递增(递减)的。
与优先级队列的区别
优先级队列无法满足标准队列结构「先进先出」的时间顺序,因为优先级队列底层利用二叉堆对元素进行动态排序,元素的出队顺序是元素的大小顺序,和入队的先后顺序完全没有关系;而优先级队列维护队列元素「先进先出」的时间顺序,又能够正确维护队列中所有元素的最值
与滑动窗口双指针的区别
滑动窗口双指针无法单凭移出窗口的那个元素更新窗口的最值
**应用:**
- [leetcode-239 滑动窗口最大值](https://leetcode.cn/problems/sliding-window-maximum/) **hard**
首先队列需要在队尾插入元素,队头移除元素,因此底层可以采用 LinkedList 数据结构;
对于队尾插入时,我们需要保证类似单调栈一样的单减特性,如果队尾元素比待插入的元素小就出队(或者从队尾到队头看是递增的);
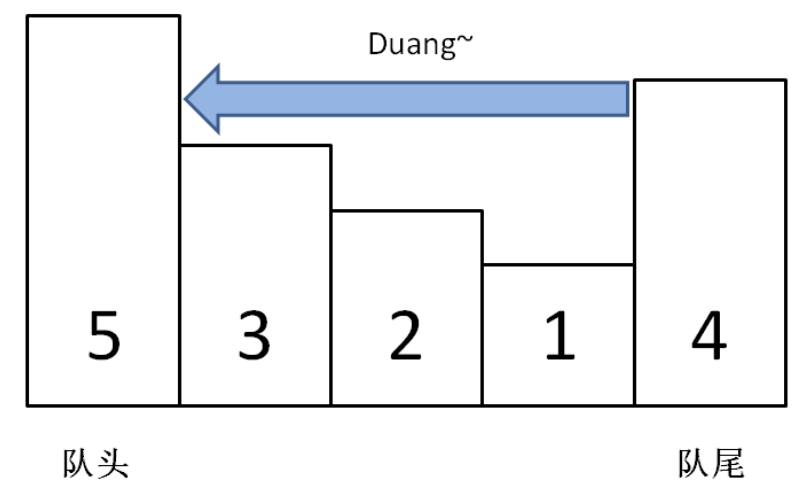
对于队头元素来说就是最大的,在出队时,还需要判断一下这个窗口最左边的元素是不是和单调队列的队头是同一个元素,如果不是就直接忽略(因为早就被移出去了)
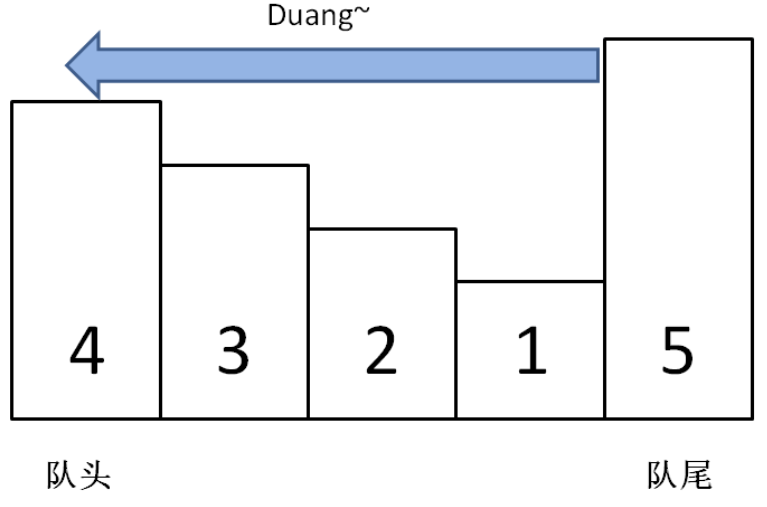
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
class Solution {
class MonotonicQueue {
private LinkedList<Integer> link;
public MonotonicQueue() {
link = new LinkedList<>();
}
public void enqueue(int val) {
while (!link.isEmpty() && link.getLast() < val) {
link.pollLast();
}
link.addLast(val);
}
public void dequeue(int val) {
if (link.getFirst() == val) {
link.removeFirst();
}
}
public int getMax() {
return link.getFirst();
}
}
public int[] maxSlidingWindow(int[] nums, int k) {
ArrayList<Integer> tmp = new ArrayList<>();
MonotonicQueue window = new MonotonicQueue();
for (int i = 0; i < nums.length; i++) {
if (i < k - 1) {
window.enqueue(nums[i]);
} else {
// 满足了窗口大小为 k
window.enqueue(nums[i]);
tmp.add(window.getMax());
// 下一次移动窗口前先出队
window.dequeue(nums[i - k + 1]);
}
}
int[] res = new int[tmp.size()];
for (int i = 0; i < res.length; i++) {
res[i] = tmp.get(i);
}
return res;
}
}
- 通用模板
其中两个链表分别维护最大元素和最小元素;还有一个链表用来维护队列的大小和时间顺序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
/* 单调队列的实现,可以高效维护最大值和最小值 */
class MonotonicQueue<E extends Comparable<E>> {
// 常规队列,存储所有元素
LinkedList<E> q = new LinkedList<>();
// 元素降序排列的单调队列,头部是最大值
LinkedList<E> maxq = new LinkedList<>();
// 元素升序排列的单调队列,头部是最小值
LinkedList<E> minq = new LinkedList<>();
public void push(E elem) {
// 维护常规队列,直接在队尾插入元素
q.addLast(elem);
// 维护 maxq,将小于 elem 的元素全部删除
while (!maxq.isEmpty() && maxq.getLast().compareTo(elem) < 0) {
maxq.pollLast();
}
maxq.addLast(elem);
// 维护 minq,将大于 elem 的元素全部删除
while (!minq.isEmpty() && minq.getLast().compareTo(elem) > 0) {
minq.pollLast();
}
minq.addLast(elem);
}
public E max() {
// maxq 的头部是最大元素
return maxq.getFirst();
}
public E min() {
// minq 的头部是最大元素
return minq.getFirst();
}
public E pop() {
// 从标准队列头部弹出需要删除的元素
E deleteVal = q.pollFirst();
assert deleteVal != null;
// 由于 push 的时候会删除元素,deleteVal 可能已经被删掉了
if (deleteVal.equals(maxq.getFirst())) {
maxq.pollFirst();
}
if (deleteVal.equals(minq.getFirst())) {
minq.pollFirst();
}
return deleteVal;
}
public int size() {
// 标准队列的大小即是当前队列的大小
return q.size();
}
public boolean isEmpty() {
return q.isEmpty();
}
}
**经典例题:**
- [leetcode-1438 绝对差不超过限制的最长连续子数组](https://leetcode.cn/problems/longest-continuous-subarray-with-absolute-diff-less-than-or-equal-to-limit/)
这道题就是单调队列 + 滑动窗口的结合:
1. 当窗口中元素极差小于等于 limit 时扩大窗口
2. 当窗口中元素极差大于 limit 时缩小窗口
3. 操作之后更新窗口大小作为最长子数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
class Solution {
public int longestSubarray(int[] nums, int limit) {
int left = 0, right = 0;
MonotonicQueue window = new MonotonicQueue();
int res = 1;
while (right < nums.length) {
window.push(nums[right]);
right++;
while (window.getMax() - window.getMin() > limit) {
window.pop(nums[left]);
left++;
}
res = Math.max(res, window.size());
}
return res;
}
class MonotonicQueue {
LinkedList<Integer> q = new LinkedList<>();
LinkedList<Integer> maxq = new LinkedList<>();
LinkedList<Integer> minq = new LinkedList<>();
public void push(int val) {
q.addLast(val);
while (!maxq.isEmpty() && maxq.getLast() < val) {
maxq.pollLast();
}
maxq.addLast(val);
while (!minq.isEmpty() && minq.getLast() > val) {
minq.pollLast();
}
minq.addLast(val);
}
public void pop(int dele) {
q.pollFirst();
if (dele == maxq.getFirst()) {
maxq.pollFirst();
}
if (dele == minq.getFirst()) {
minq.pollFirst();
}
}
public int getMax() {
return maxq.getFirst();
}
public int getMin() {
return minq.getFirst();
}
public int size() {
return q.size();
}
public boolean isEmpty() {
return q.isEmpty();
}
}
}
- [leetcode-862 和至少为 K 的最短子数组](https://leetcode.cn/problems/shortest-subarray-with-sum-at-least-k/) **hard**
[leetcode-209 长度最小的子数组](https://leetcode.cn/problems/minimum-size-subarray-sum/)
这道题需要结合 前缀和、滑动窗口和单调队列的思路。利用前缀和可以求得子数组和(大于 k 时滑动窗口满足缩小条件),滑动窗口辅助定位什么时候前缀和**减去最小元素值**仍然是 ≥ k 的,即为满足条件的情况
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
class Solution {
public int shortestSubarray(int[] nums, int k) {
int n = nums.length;
// 前缀和
long[] preSum = new long[n + 1];
preSum[0] = 0;
for (int i = 1; i <= n; i++) {
preSum[i] = preSum[i-1] + nums[i-1];
}
MonotonicQueue window = new MonotonicQueue();
int left = 0, right = 0;
int len = Integer.MAX_VALUE;
while (right < preSum.length) {
window.push(preSum[right]);
right++;
// 这里最后一轮 right 会越界
while (right < preSum.length && !window.isEmpty() && preSum[right] - window.getMin() >= k) {
len = Math.min(len, right - left);
window.pop();
left++;
}
}
return len == Integer.MAX_VALUE ? -1 : len;
}
class MonotonicQueue {
LinkedList<Long> q = new LinkedList<>();
LinkedList<Long> maxq = new LinkedList<>();
LinkedList<Long> minq = new LinkedList<>();
public void push(long val) {
q.addLast(val);
while (!maxq.isEmpty() && maxq.getLast() < val) {
maxq.pollLast();
}
maxq.addLast(val);
while (!minq.isEmpty() && minq.getLast() > val) {
minq.pollLast();
}
minq.addLast(val);
}
public void pop() {
long del = q.pollFirst();
if (del == maxq.getFirst()) {
maxq.pollFirst();
}
if (del == minq.getFirst()) {
minq.pollFirst();
}
}
public long getMin() {
return minq.getFirst();
}
public long getMax() {
return maxq.getFirst();
}
public int size() {
return q.size();
}
public boolean isEmpty() {
return q.isEmpty();
}
}
}
- [leetcode-918 环形子数组的最大和](https://leetcode.cn/problems/maximum-sum-circular-subarray/)
这道题考察的是环形数组的子数组和,我们仍然可以沿用之前的思路,将环形数组展开成线性的 2 倍长度。但是题目给了限制子数组长度不能超过 nums.length,因此还需要借助滑动窗口来控制窗口大小,在每次入队时更新子数组和最大值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
class Solution {
public int maxSubarraySumCircular(int[] nums) {
int n = nums.length;
long[] preSum = new long[2 * n + 1];
preSum[0] = 0;
for (int i = 1; i < preSum.length; i++) {
preSum[i] = preSum[i-1] + nums[(i - 1 + n) % n];
}
MonotonicQueue window = new MonotonicQueue();
// 第一个前缀和
window.push(0);
long len = Integer.MIN_VALUE;
for (int i = 1; i < preSum.length; i++) {
// 减的时候尽量不要减太多,也就是减最小值
len = Math.max(len, preSum[i] - window.getMin());
if (window.size() == nums.length) {
window.pop();
}
window.push(preSum[i]);
}
return (int) len;
}
class MonotonicQueue {
LinkedList<Long> q = new LinkedList<>();
LinkedList<Long> maxq = new LinkedList<>();
LinkedList<Long> minq = new LinkedList<>();
public void push(long val) {
q.addLast(val);
while (!maxq.isEmpty() && maxq.getLast() < val) {
maxq.pollLast();
}
maxq.addLast(val);
while (!minq.isEmpty() && minq.getLast() > val) {
minq.pollLast();
}
minq.addLast(val);
}
public void pop() {
long del = q.pollFirst();
if (del == maxq.getFirst()) {
maxq.pollFirst();
}
if (del == minq.getFirst()) {
minq.pollFirst();
}
}
public long getMin() {
return minq.getFirst();
}
public long getMax() {
return maxq.getFirst();
}
public int size() {
return q.size();
}
public boolean isEmpty() {
return q.isEmpty();
}
}
}
- **TODO:** 需要用到动态规划
[leetcode-1696 跳跃游戏 VI](https://leetcode.cn/problems/jump-game-vi/)
[leetcode-53 最大子数组和](https://leetcode.cn/problems/maximum-subarray/)
[leetcode-1425 带限制的子序列和](https://leetcode.cn/problems/constrained-subsequence-sum/)
- [leetcode-1429 第一个唯一数字](https://leetcode.cn/problems/first-unique-number/)
这题主要考察 哈希表和队列的配合使用,我们通过哈希表来记录数组中元素出现的次数,队列来保持元素的先后顺序。在查找唯一元素时,对于队列中不唯一的元素,因为始终不满足题意,因此直接删去即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class FirstUnique {
private HashMap<Integer, Integer> count = new HashMap<>();
private LinkedList<Integer> q = new LinkedList<>();
public FirstUnique(int[] nums) {
for (int num : nums) {
add(num);
}
}
public int showFirstUnique() {
while (!q.isEmpty()) {
int v = q.peek();
if (count.get(v) > 1) {
q.poll();
} else {
return v;
}
}
return -1;
}
public void add(int value) {
q.offer(value);
int v = count.getOrDefault(value, 0);
count.put(value, v + 1);
}
}