Algorithms I & II
最后更新时间:
Algorithms I & II
Ch1 Union-Find
非优化版本

优化1 quick find


优化2 weighted quick find
总体思想即维护并查树不要过高,每次合并时让小的在下面


优化3 path compression

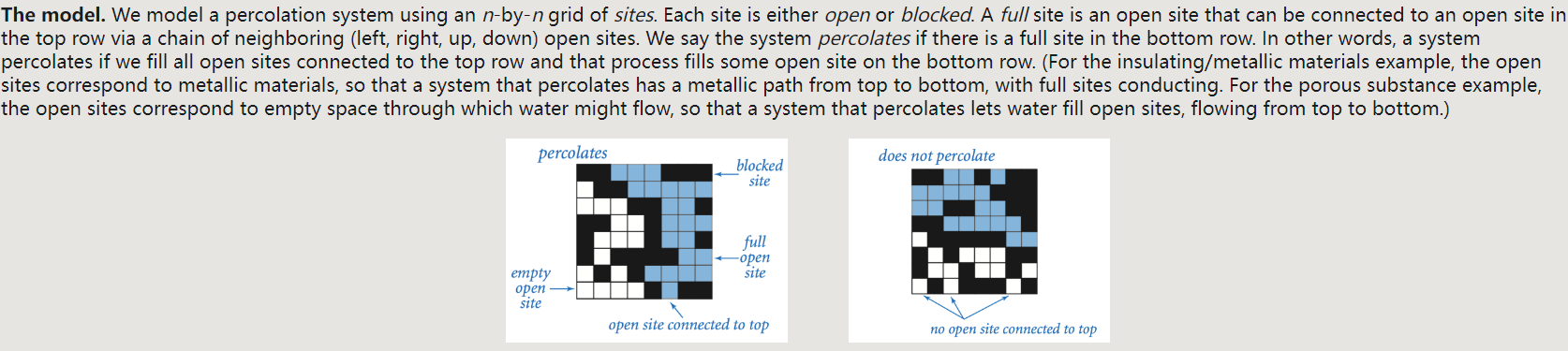
Project1: Precolation
题目链接:Programming Assignment 1: Percolation
写在前面
本来觉得这门课就是单纯再学一遍算法,但是真正做了项目才知道自己在算法与如何应用之间还存在着不小的差距。这门课从如何去设计计算机模型、如何去使用算法、如何去规范编写程序以及测试程序上都给出了练习。相信练完之后对工程化代码的能力能有不小提升。
题面简介
题目本身不难,主要是以并查集搜索为背景的物理渗透模型,需要学生去模拟寻找阈值,即能使得整个系统渗透(从最上部流到最下部)的最小连通数。并以此计算均值、方差和置信区间。
拟解决的问题
- 题目已给出了可用来快速并查的集合对象,怎么应用到此物理渗透系统上?即如何设计数据结构?
- 根据题意,整个系统联通的意思是最上端与最下端联通,如何表示?
- 对于测试某一个站点的联通性,如何表示?
解决思路:
先来分析一下题目给的
WeightedQuickUnionUF类,可以看到内部为一维数组结构,对于我们的 n x n 网络,是无法直接表示的,因此这里需要作二维到一维的映射(注意看题目说了编号从 1 开始)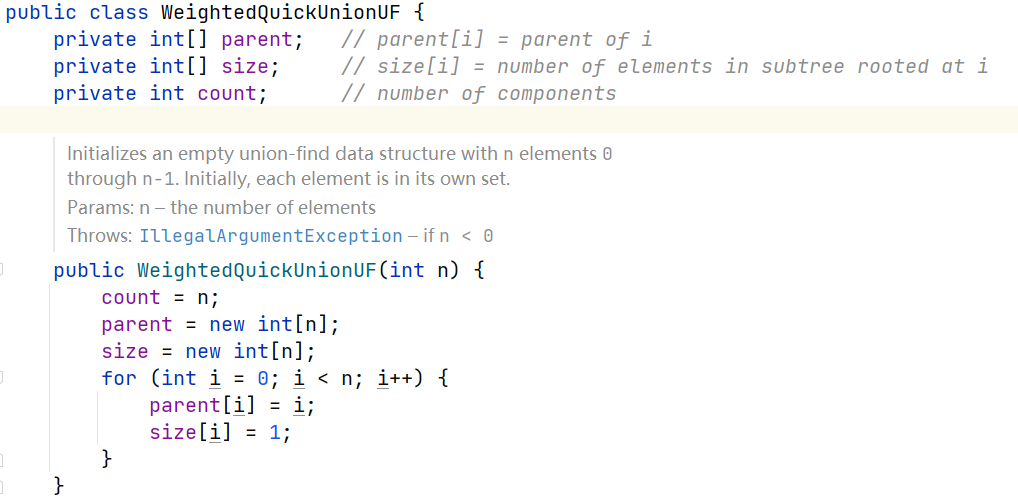
根据 tips,我们可以在最上端和最下端增设两个虚拟站点 0 和 n + 1, 一旦有最上端或最下端的站点开放,就将其与虚拟站点合并。
这样整个系统的连通性就可以转换为判断上下两个虚拟站点是否连通
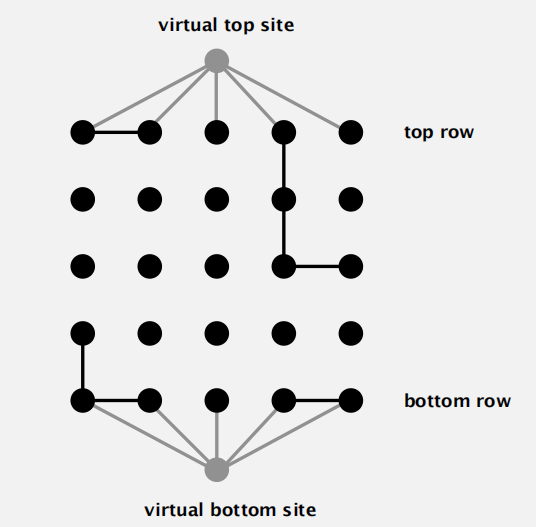
根据题意:
A full site is an open site that can be connected to an open site in the top row via a chain of neighboring (left, right, up, down) open sites.
可知只需要判断指定站点和上面虚拟站点的连通性即可。这里会遇到的一个问题是:
https://github.com/PKUFlyingPig/Princeton-Algorithm
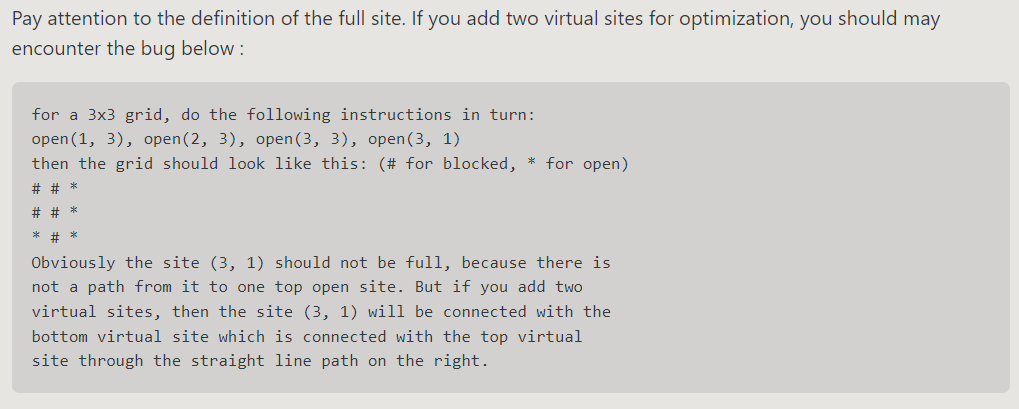
因此可以再单独维护一个只连通上面虚拟结点的并查集即可。
总体


Analysis of Algorithms
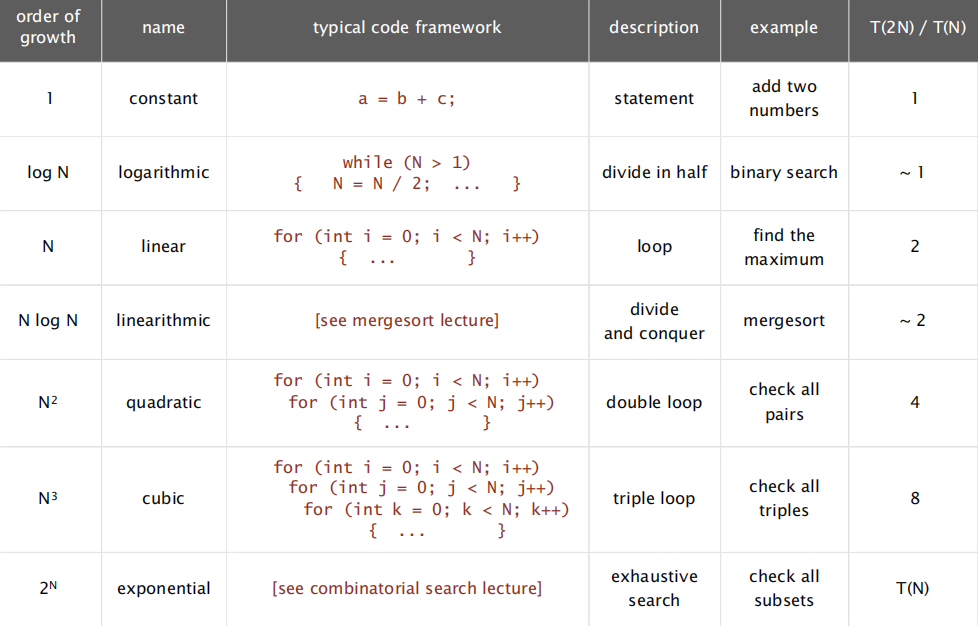
Ch2 Stacks and Queues
generics
不需强制类型转换;避免运行时错误;
注:Java 不支持泛型数组
wrapper type. autoboxing

Iterators
遍历机制:实现 Iterable 接口(返回 Iterator 类方法的接口,后者是包含
hasNext()和next()方法的类)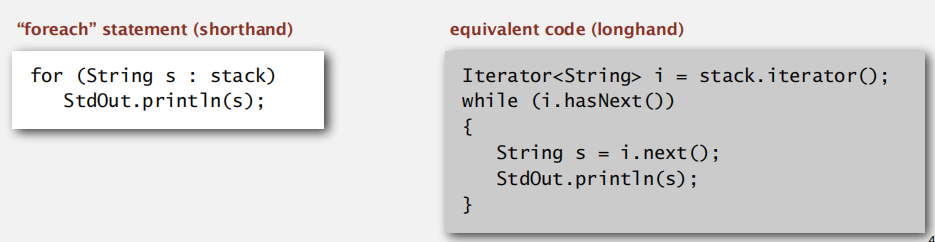
Project2: Deques and Randomized Queues
第一部分要求实现双端队列,并在常数时间内在头尾实现增删元素功能
为了能在尾部也实现常数时间增删,采用循环双链表结构(对于单链表,增可以利用 last 指针,但是删只能遍历),将头尾相接,不需额外设立 first 和 last 指针就可以快速索引至头尾元素处
同时为了避免判断边界条件,增加 dummy 结点,使得第一个元素可以当做普通元素来用
第二部分要求实现随机数据结构(用队列或栈都可),在迭代和弹出元素时均要求满足随机性,入队出队均常数时间,迭代器的构造函数可以线性时间
由于这部分对于元素的检索(随机访存)要求较高,因此内部采用数组结构
首先对于随机性,
StdRandom.uniformInt**可以很好的获得指定区间的随机数,但是这里面临的挑战时,如何保证弹出时也是随机的同时比较好维护数组空间;另外,在实现迭代器时如何保证只会获取一次数组中的元素对于第一个问题,结合栈思想每次在栈顶删除元素,可以每次将制定删除的随机元素交换至栈顶再出去,这样仍然可以保证数组内部的连续性;
对于第二个问题,题目给出了提示迭代器的构造函数可以在线性时间内完成,因此可以额外开辟一个待遍历的数组,数组元素内容与原空间一致,利用
StdRandom.shuffle来以数组为单位打乱顺序,这样可以保证每创建一个迭代器,其内部元素顺序均不同bugs 修复:测试样例中 deque API 爆错:
java.lang.ArrayIndexOutOfBoundsException: Index 0 out of bounds for length 0这是由于在实现
resize缩容时并未对大小作限制,使得 capacity 可以降到 0

Elementary Sorts
选择排序
特点:即使元素已排好序,仍会遍历从左向右扫描,时间复杂度稳定在
O(n^2)插入排序
由于待排序元素左边均有序,所以只需要依次和左边的元素比较即可
其时间复杂度取决于输入元素的状态
最优情况是已排好序状态,线性时间比较;最坏情况是降序排序,平方时间比较+排序
逆序对 ⇒ 引出部分排序性质的定义

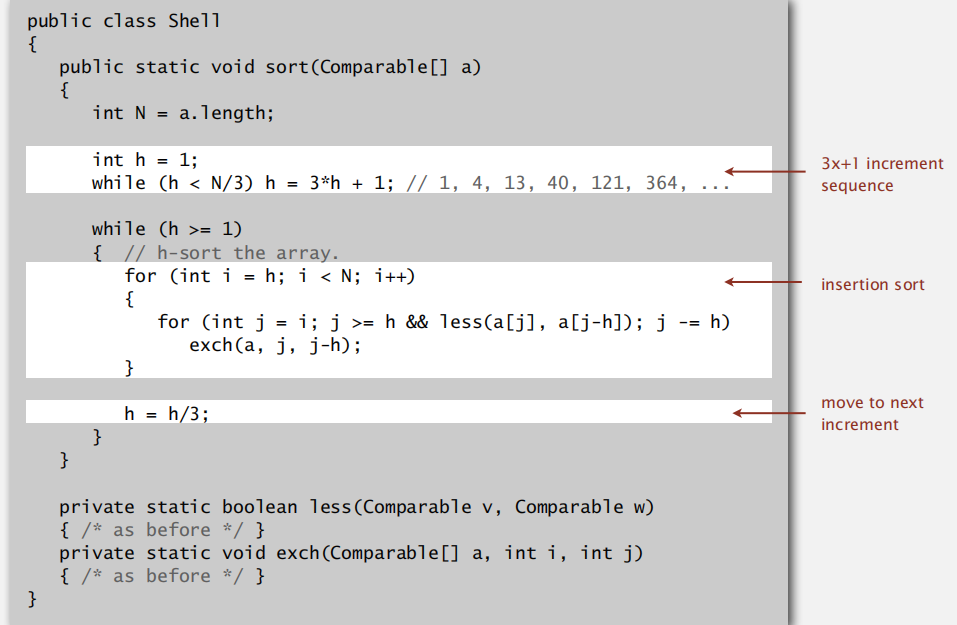
希尔排序
按照步长 h 划分子序列,子序列内部插入排序
每轮 h 逐步减少(不一定是每次减少1)
为什么选择?

h 如何选择?

Java Code
Application
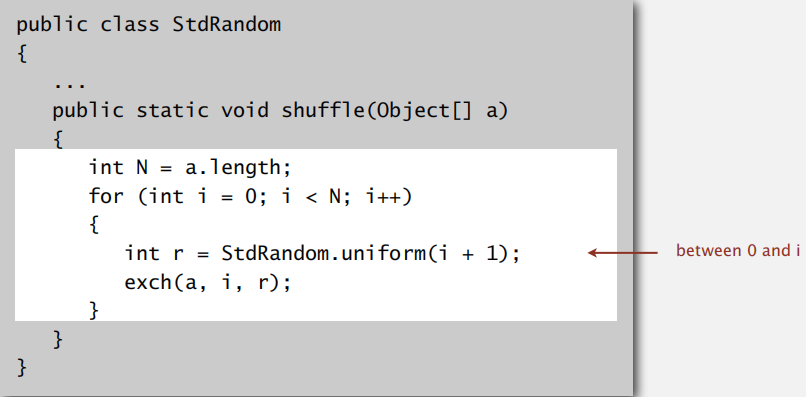
Knuth shuffle

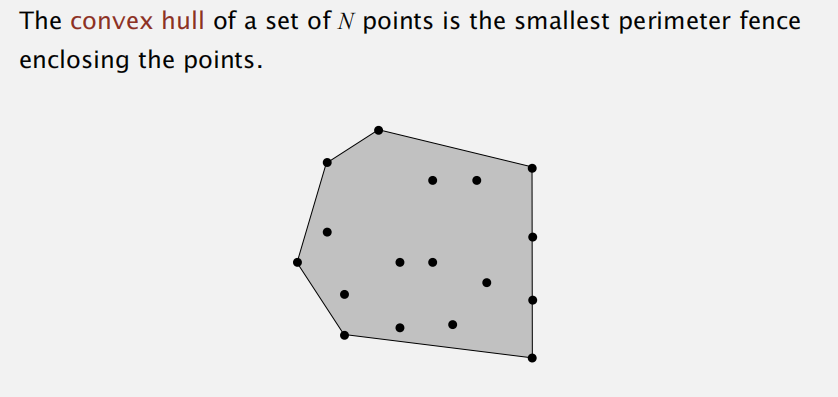
Convex Hull
凸包的定义
两个几何性质
- 逆时针遍历凸包点可以回到起点
- 按照 y 轴最低的包点作为参照,其他的凸包点相对之的极角度顺序递增
Graham scan algorithm

第三步指的是如果无法构成逆时针路径就排除上一个选择的凸包点
实现如何判断逆时针?
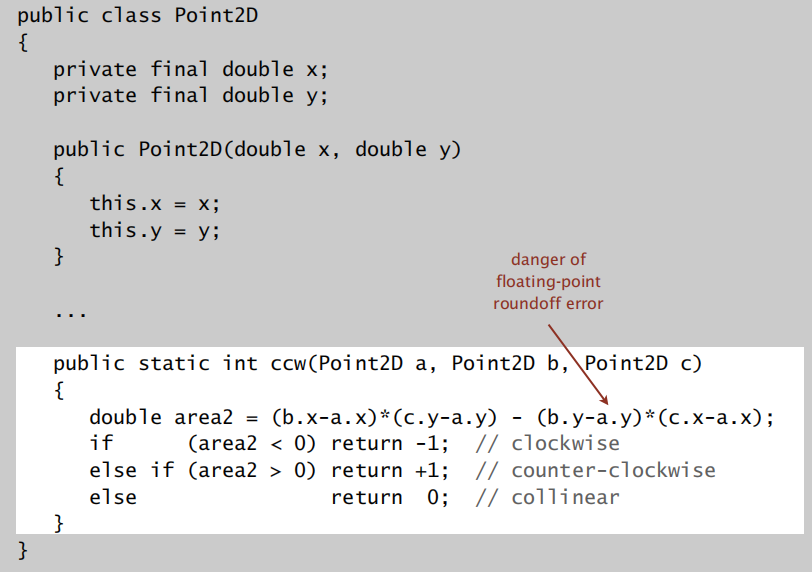
其数学知识基于下面:

整体实现

Ch3 Mergesort
mergesort
相应改进:
划分成小数组时可以选择插入排序
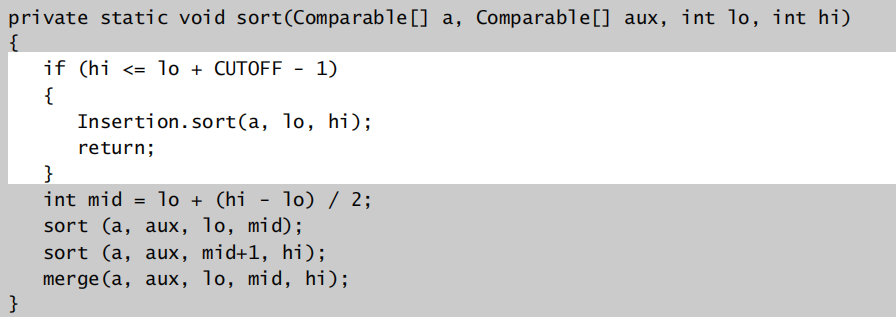
在对子数组排序后,判断左边数组的最大值是否已经小于右边数组的最小值,如果是的话可以直接返回,不再进行归并操作
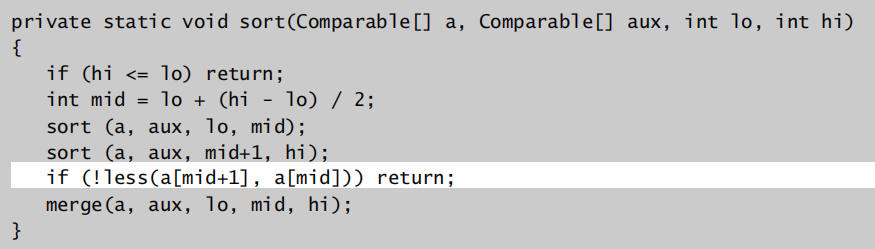
自下而上非递归实现归并排序


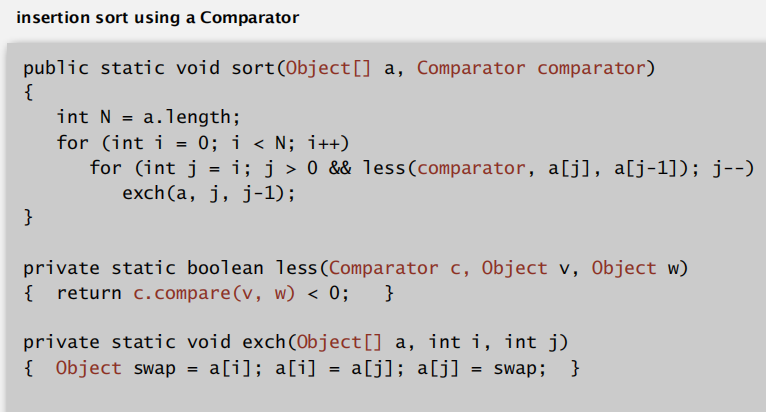
comparators
针对同一类型的数据,也可以支持不同的比较原则
稳定性
插入排序
当比较元素相等时,不再发生元素交换,因此是稳定的
选择排序
元素交换存在跨间隔,因此会引发不稳定

归并排序
取决于合并子数组时,两个相等元素如何合并的情况,如果是优先左数组的话则是稳定的
Project3: Collinear Points
- 感觉自己还是对于 API 的使用以及各种算法的应用比较生,需要多加练习才会知道怎么综合运用才能省时省力,同时减少冗余代码
题面:
题目给定了点和线段的定义,需要我们在诸多点的集合当中寻找所有的共线点出来
同时题目给出了两种求解思路:暴力法和排序搜索法
求解思路1:暴力法
这个比较好说,也就是根据定义(此时共线定义是满足4个点,两两之间斜率相等即可),4次方遍历结点,找到所有满足条件的点放入结果集当中。
需要注意结果集中不能有重复的线段出现(即线段中四个点只能出现一次,最好就是放两端的点)
因此根据这个要求,我们可以进一步做一些优化,通过提前将点按照大小规则排好序,再去遍历,即可相对快速方便的把两端点找出
排序搜索法
观察到性质:共线的点满足斜率相等。那么我们就可以依次枚举每一个点作为参考点,对其他点求相对其的斜率,排序后会发现斜率相等的点将会集中起来(如果斜率相等点满足共线点个数要求,那么就对应一个线段),这样可以更快速地找出所有共线来
拟解决的问题及对应方案:
如何判断共线条件
这里共线条件已经变成了 4 个点及以上满足斜率相等。因此每次排好序后,第一个点当然是参照点本身,因此从第二个点开始搜索,往后遍历判断当前斜率相等的点是否大于等于3,是则符合一对线段。否则继续判断下一个斜率的线段
注:对于排序,因为我们在 Point 类中已经实现了一个针对斜率比较的比较器,因此可以直接调用
Arrays.sort(tmp, origin.slopeOrder());而无需自己再重复写一遍如何解决重复问题
由于我们会将所有点作为参照进行遍历,那么势必会出现重复判断的情况,如何保证结果集中的元素唯一呢?
这就要求对存储数据作要求,即每次存入的点左端点是最小值,右端点是最大值,这样一定就不会有重复的点出现(因为 point 集元素唯一,因此最小值点只会出现一次,我们可以等参考点遍历到最小点时再放入结果集中)
**bug fix**:为了快速遍历到最小点,我们也依照暴力法优化,先对 point 集按照大小作排序,然后再依次作参考点遍历。这里由于又会排序一遍,如果两次排序用同一数组原地操作,那么会出现死循环的情况,所以一定要额外建立一个备份数组

QuickSort
qucik sort
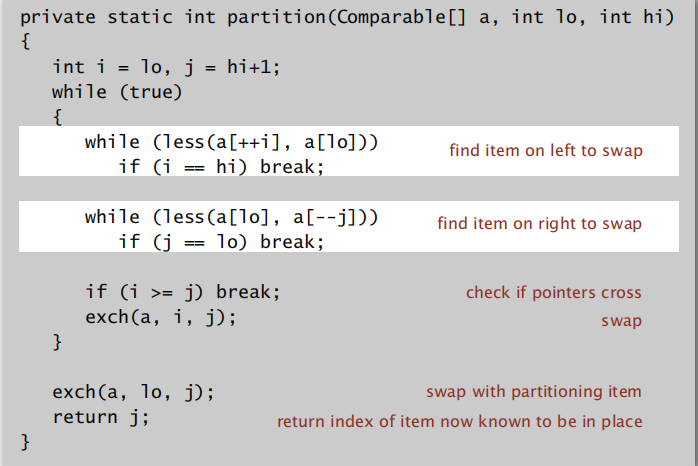
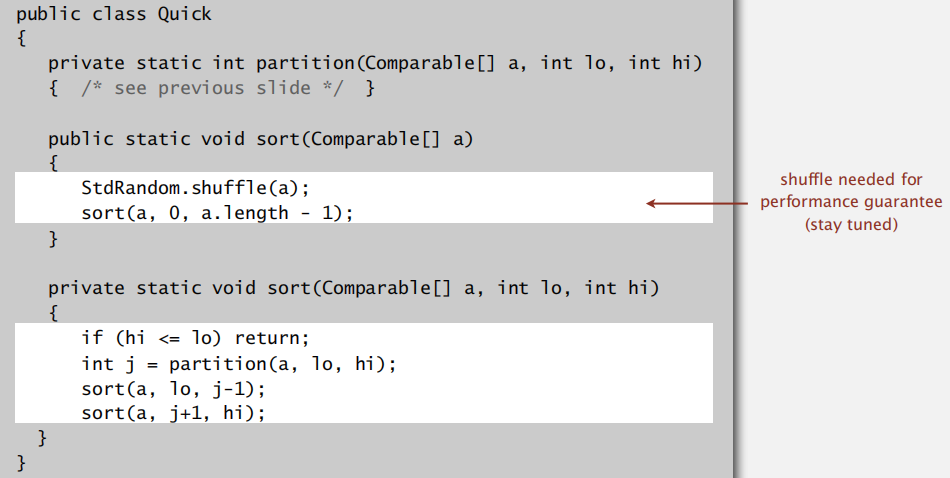
实现性能保障的前提:数组在排序之前应先 shuffle 一下,这样可以使得每次 partiton 之后,左右子数组的顺序仍然是随机的
算法实现改进1
与归并排序一样,针对划分之后的小数组可以直接插入排序
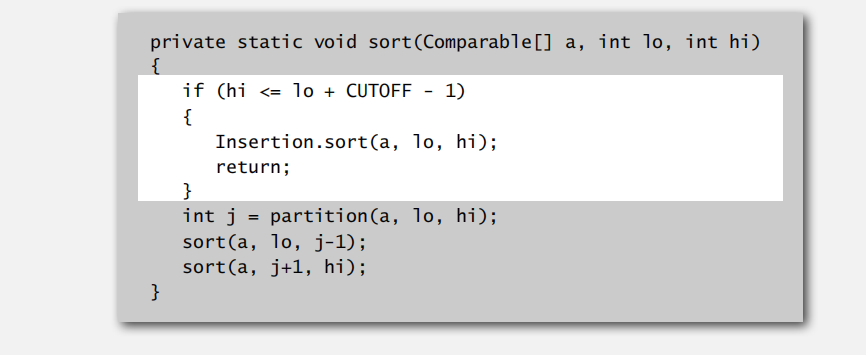
算法实现改进2
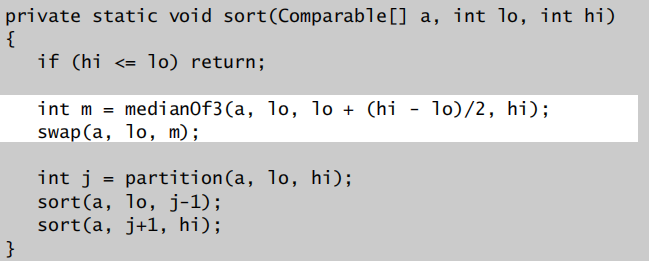
采样中间值
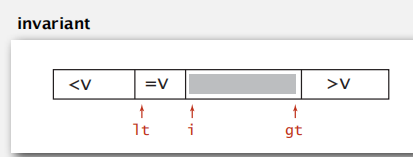
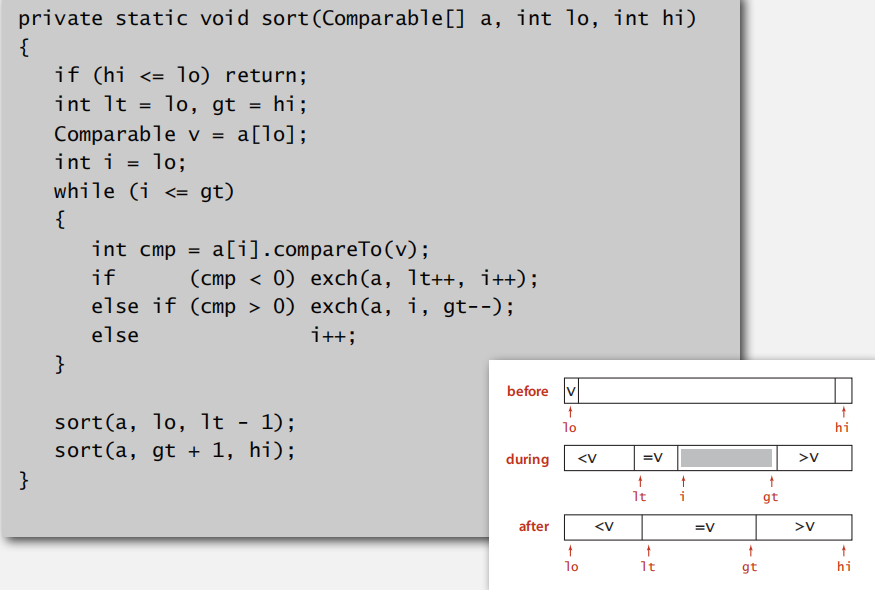
Dijkstra 3-way partitioning

这样可保证 lt 左边的均小于 v;gt 右边的均大于 v,lt 和 i 之间的相等
代码实现:
Ch4 Priority Queues
数据的不变性
Immutable: 诸如 String 以及一些包装类都是不可变数据类型
mutable: StringBuilder, Stack
堆排序
只需要上浮操作即可,
与其他排序算法相比,其具有稳定的时间复杂度以及支持原地操作

但是不具有稳定性,且不适用于缓存结构系统,(其数组索引涉及整个大数组)
Project4: 8 Puzzle
- 题目理解: 以启发式搜索为背景,解决 puzzle 移动问题。其中每一步的权重由曼哈顿距离(或汉明距离)与当前搜索步数的和决定。本质上是利用优先级队列作 BFS 探索最短路径问题
- 这道题整体设计上并不难,主要在一些细节的地方上需要注意,同时自己对于面向对象编程、封装意识还是薄弱,多加练习
需要注意的细节:
不可求解的情况,题面中也给出了提示,即 twin 可以达到目标状态,而初始状态不可到达的情况,所以这里需要在作 BFS 时判断避免死循环
1
2
3
4if (minBoard.manhattan() == 2 && minBoard.twin().isGoal()) {
solvable = false;
break;
}这里保存状态是在初始化 solver 时即进行,否则 API
moves以及isSolvable结果是不可知的,按照这个思路加题面提示每次记录当前搜索状态以及前一搜索状态,我们在solution上可以反向溯源至初始状态,返回Iterable<Board>为此,可以进一步封装一层 Board 类,同时记录其前一节点、当前步数以及优先级值以便作优化
注意在作启发式搜索时,对于 neighborhoods 我们不能全部放入队列当中,需要考虑到前一状态是否已经探索的情况
1
2
3if (preBoard != null && preBoard.board.equals(neighbor)) {
continue;
}


Elementary Symbol Tables
如何实现类的 equals 方法?
不仅要考虑字段的值大小,还要比较类型是否一样、是否为空的情况

递归实现二叉树插入操作
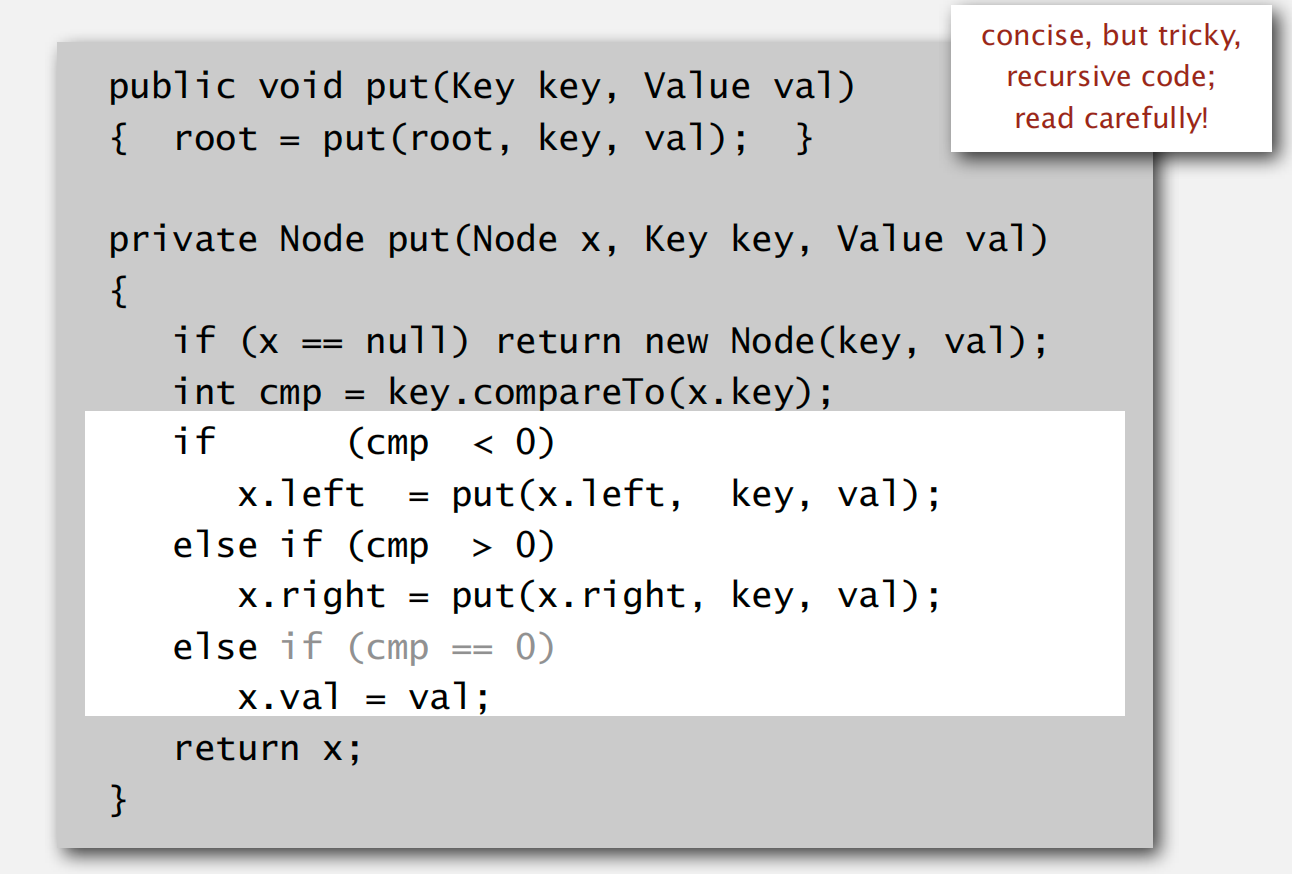
注意返回后赋值操作的 left operand 是什么
如果插入元素大小随机,那么类比与快速排序之前的 shuffling ,将会有
2lnN的平均时间复杂度以及4.311lnN的最坏时间复杂度
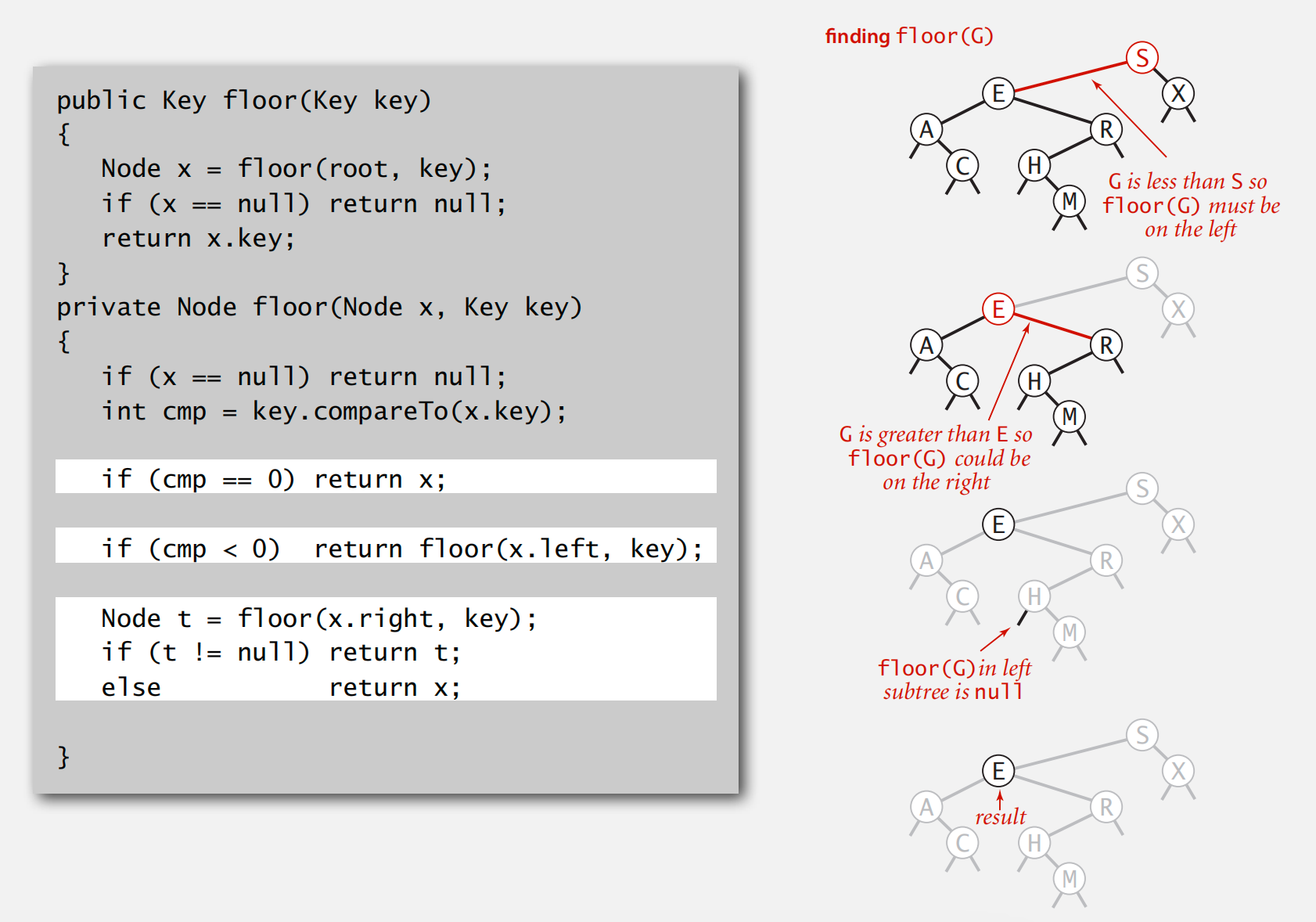
二叉搜索树实现符号表 floor 操作
即找到第一个最大的小于元素的 node,如果指定元素比当前节点小,则一定在其左子树中;如果比当前元素大,则需进一步筛查右子树中是否还有比指定元素小的,若没有则当前元素就是结果,否则仍需递归右子树
二叉搜索树实现符号表 deletion 操作
deleMin 左下节点元素值最小

Hibbard deletion 删除指定元素
寻找并与指定元素的后继节点替换,之后删除掉指定元素节点
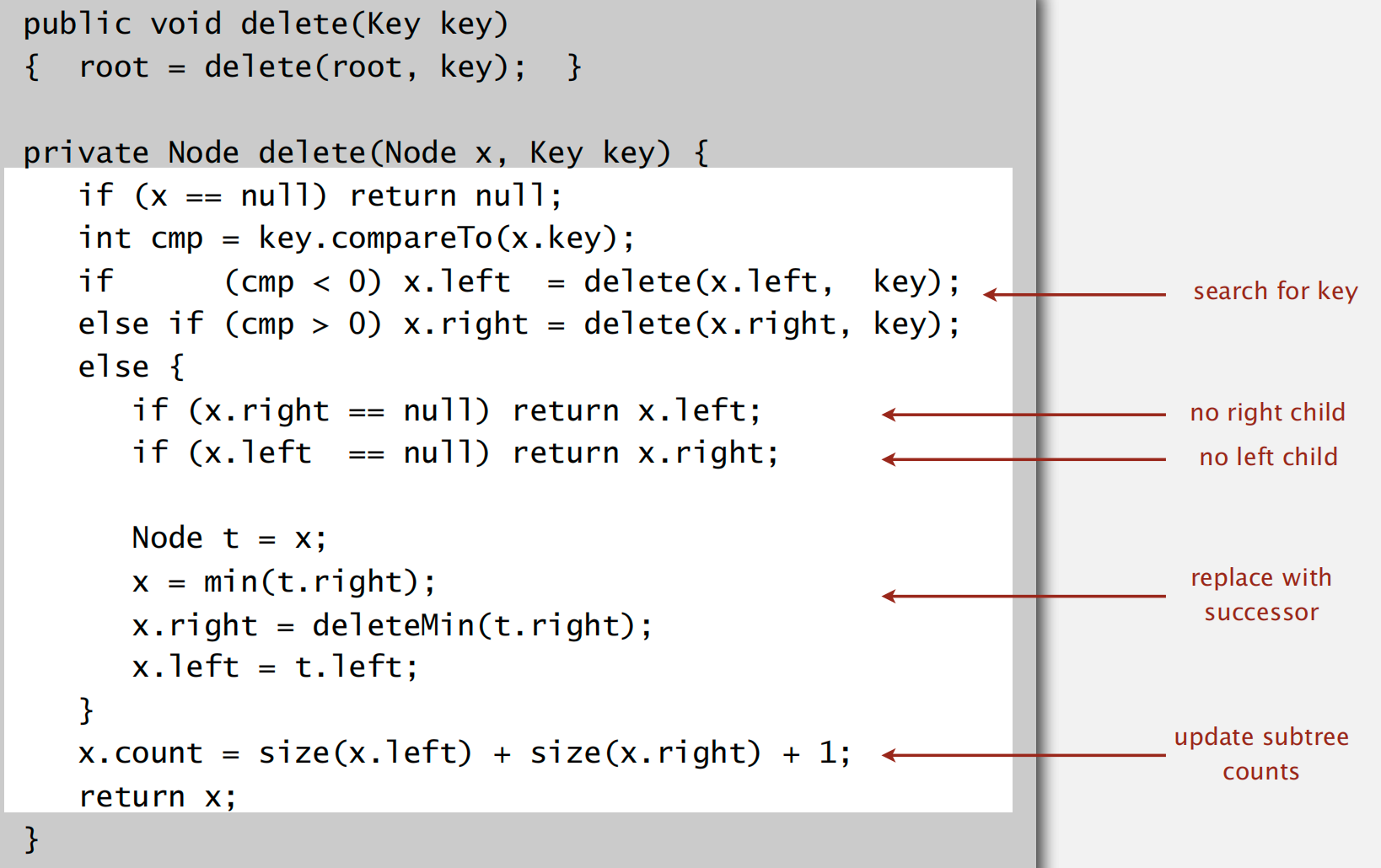
缺点:这种删除方式在大量随机插入和删除节点之后会导致二叉树平衡性降低,复杂度由 logN 增至 sqrt(N)
Ch5 Balanced Search Trees
2-3 tree
definition:
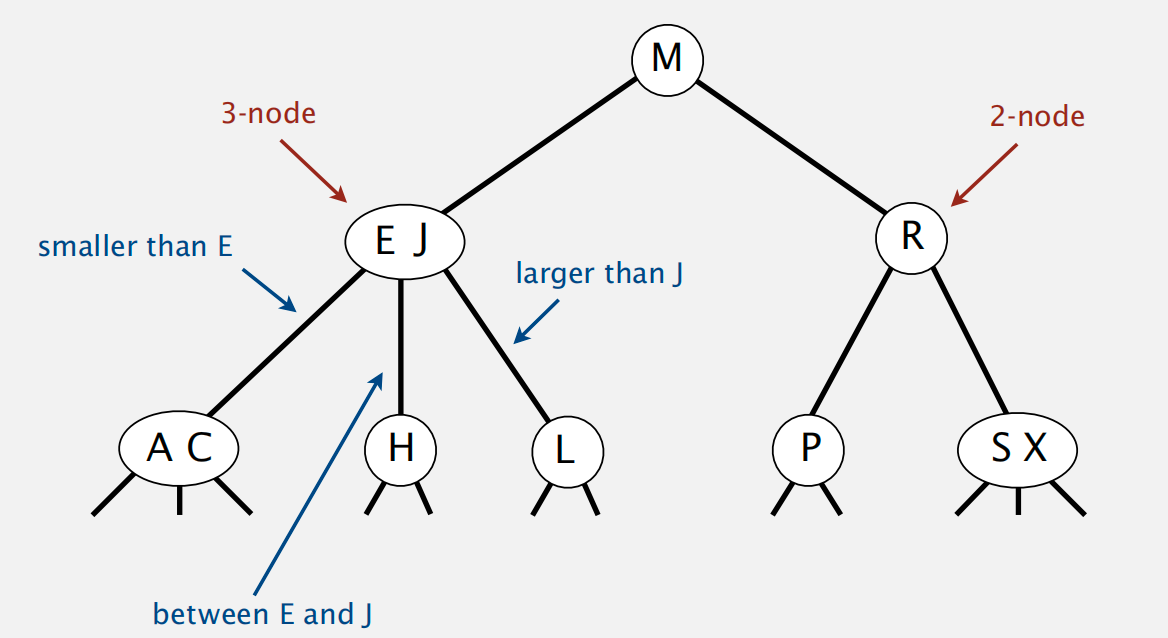
insert operation:
- for 2 node point: 直接插入到 2node 点上即可,变为 3node point
for 3 node point: 直接插入将会变为 4node 点,因此需要将中间节点递归上移至父节点中直至符合定义
注:根节点的分裂将导致树的高度 +1
变换的操作只是先创建一个临时的4node,再将其分裂为2个2node,中间节点上移
Red-Black BSTS
left-leaning red-black BSTs
基于 2-3 BSTS 所作改进:
- 将 2-3tree 视作 BST
use a internal link in the 3node,which larger point to smaller
properties: 与 2-3 tree 对应,实际上将每一个 red links 水平化并节点合并后就对应为了 2-3 tree

search op code:as same as the BST
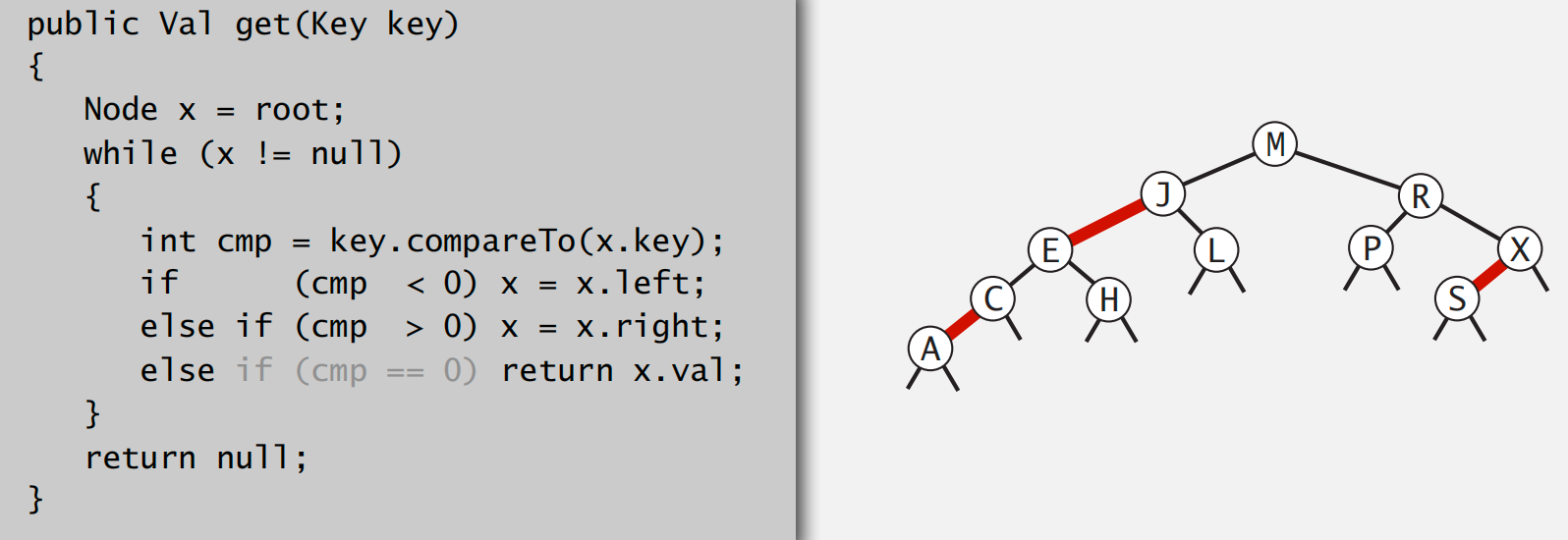
how to represent a red-black tree
color 指示的是当前节点的入边 color
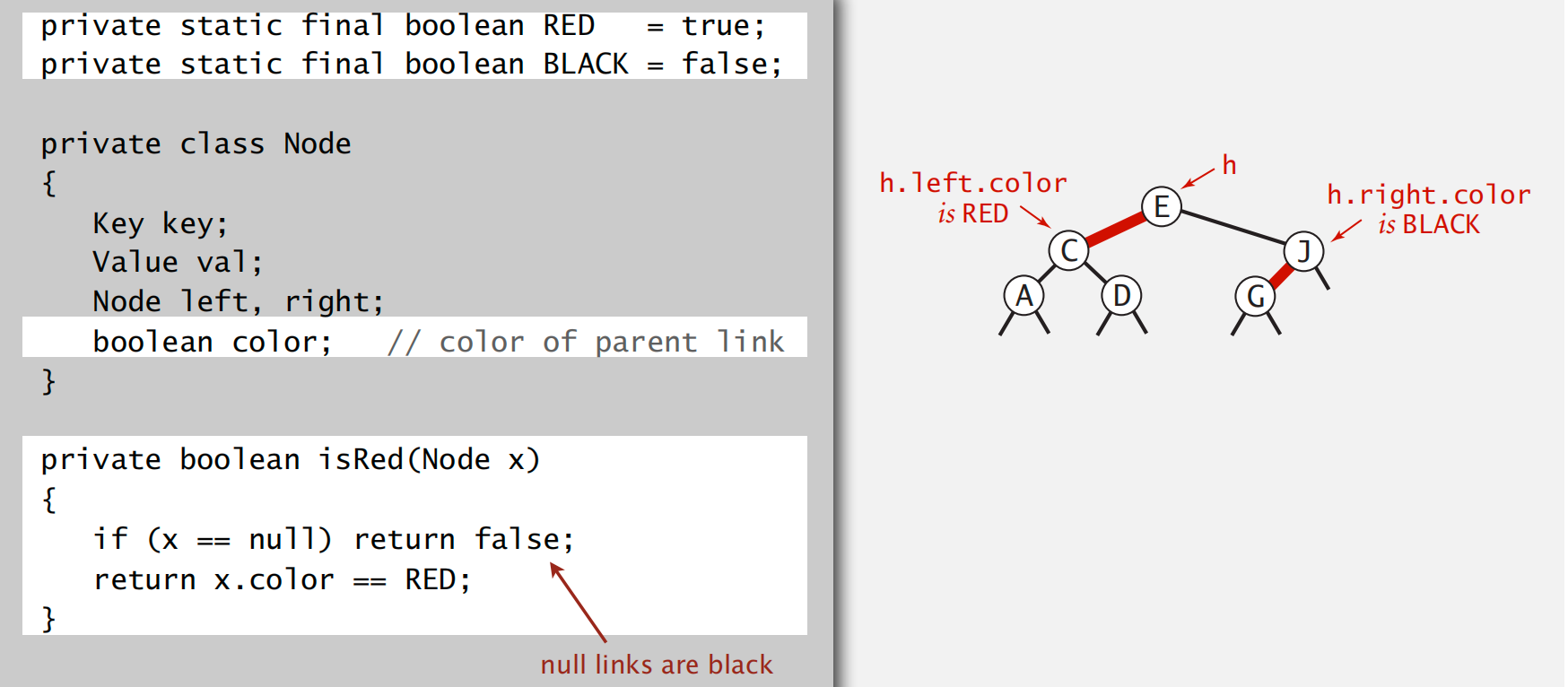
对于所有空节点,其 color 也是 black
Left rotation operation
当 red link 不满足左倾条件时,需要进行左旋调整

of course, 有时需要临时作右倾操作,code 是对称的

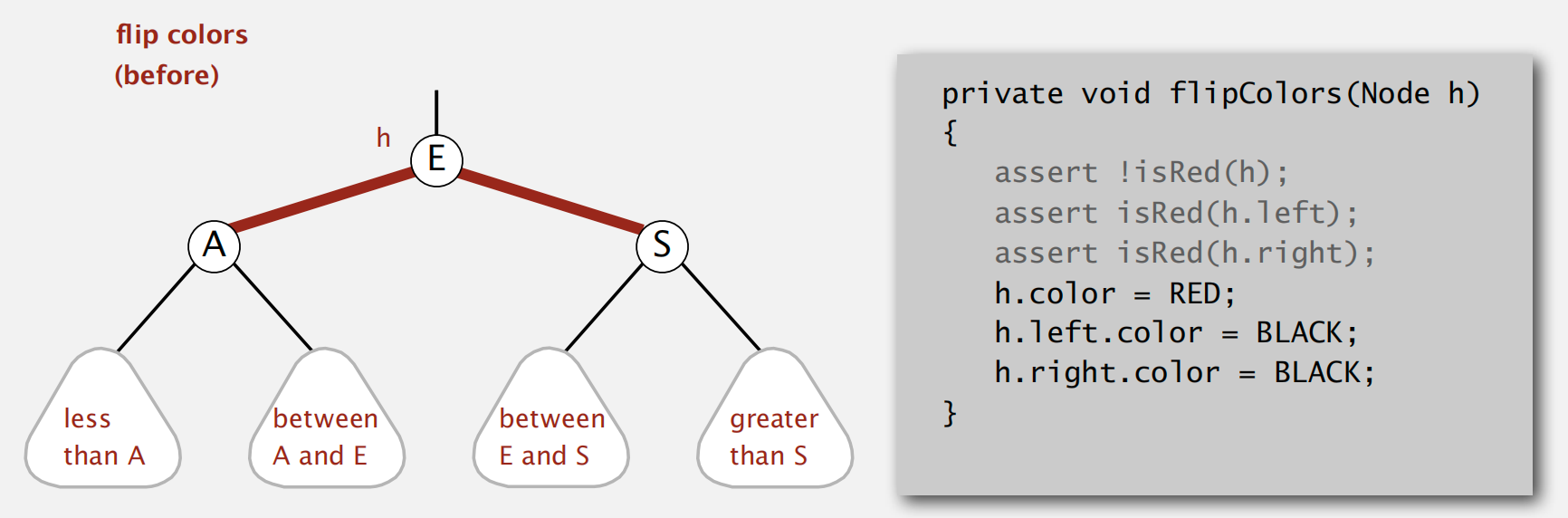
color flip operation
当出现 red link 相连的情况,对应 2-3 tree 中的 4node
basic strategy: 与2-3 tree insert node 节点对应一致,并调整 red links 的倾向
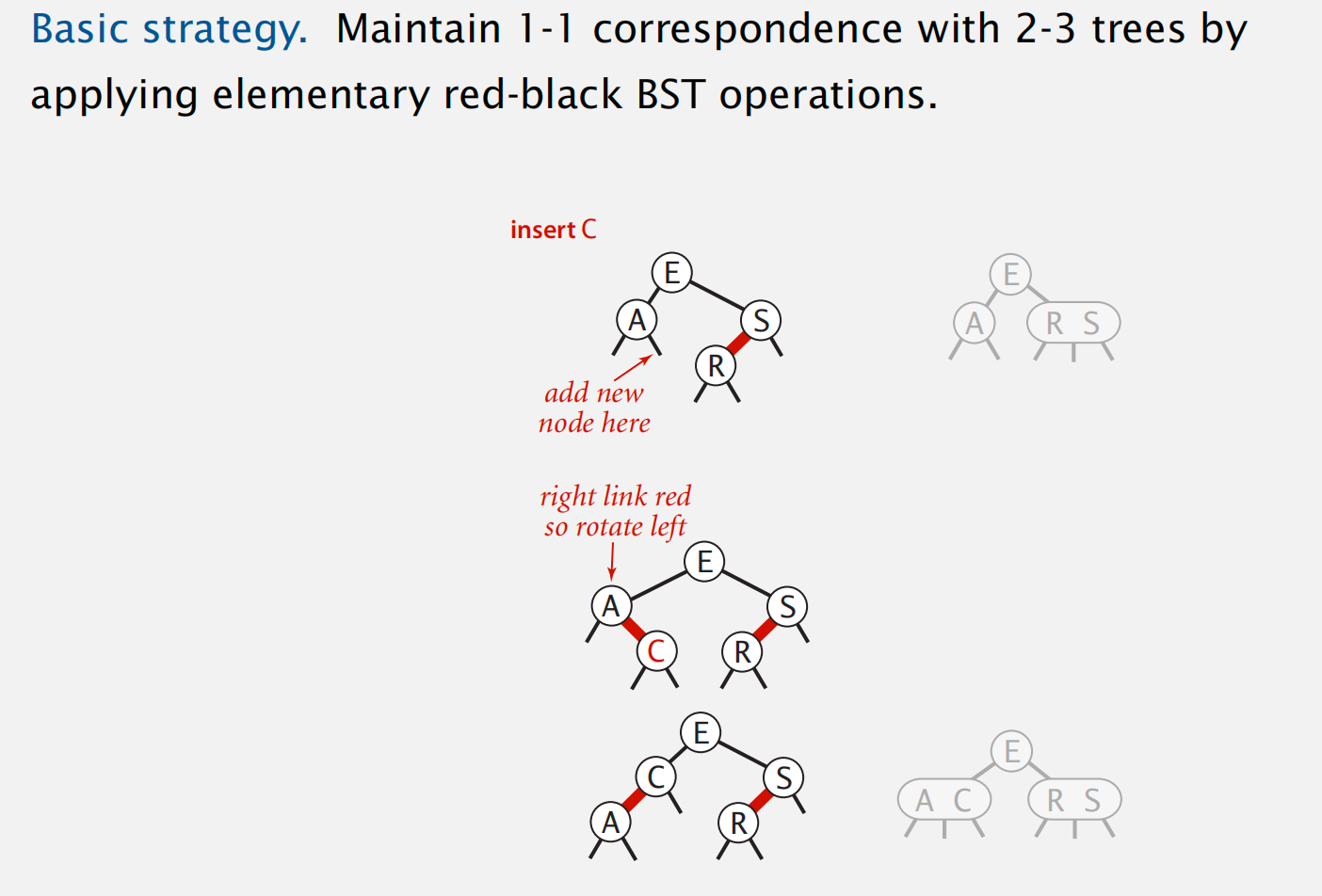
summer: 3 cases for insert a node

递归实现:

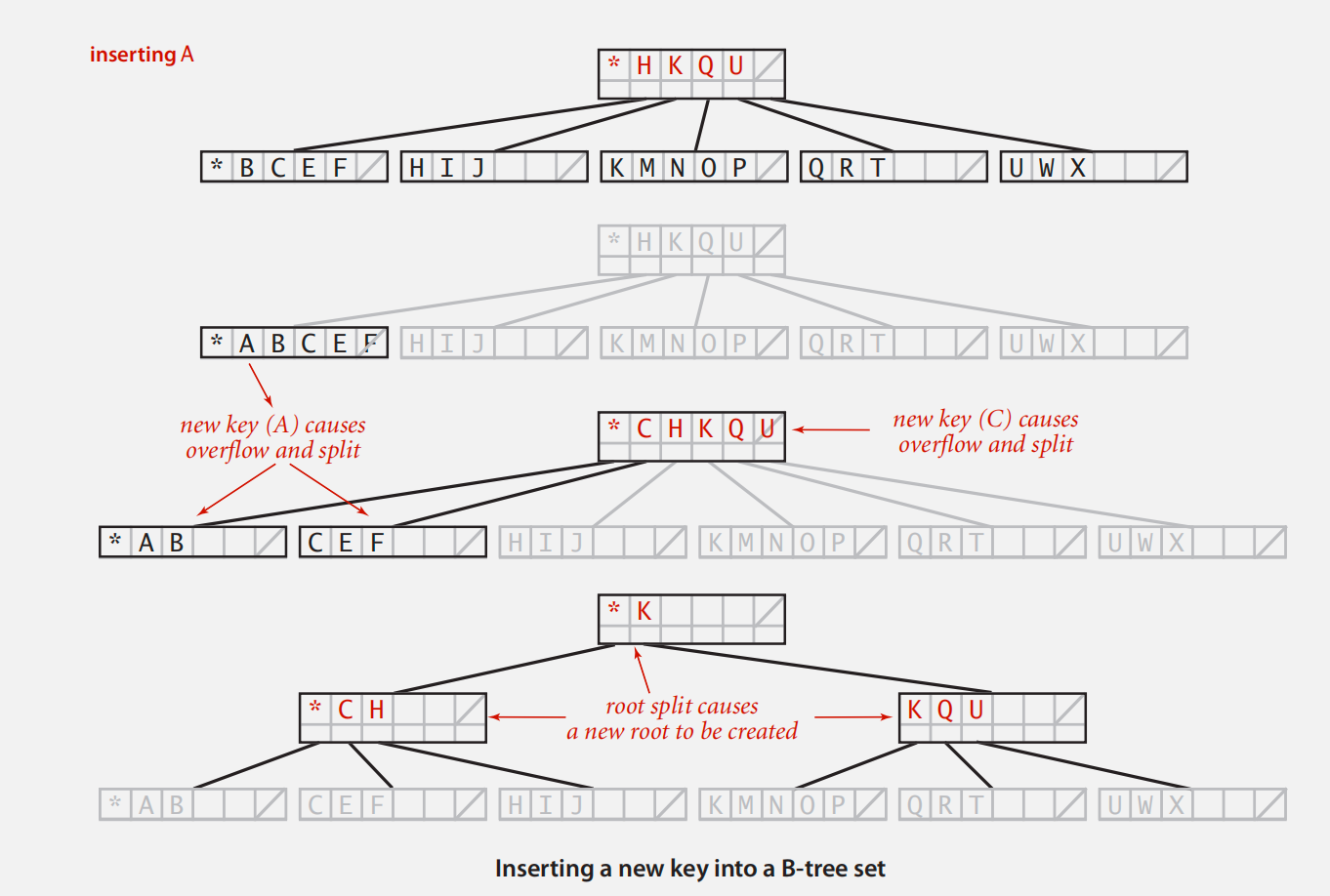
B-tree
definition:

注解:每个内部节点标识了指向目标节点的下一链接位置应该在哪里
insert a node: 当节点数量达到 M 时,需要分割节点,并将索引键上移
也就是说,每个节点中元素数量在 M - 1 ~ M / 2 之间
Geometric Applications of BSTs
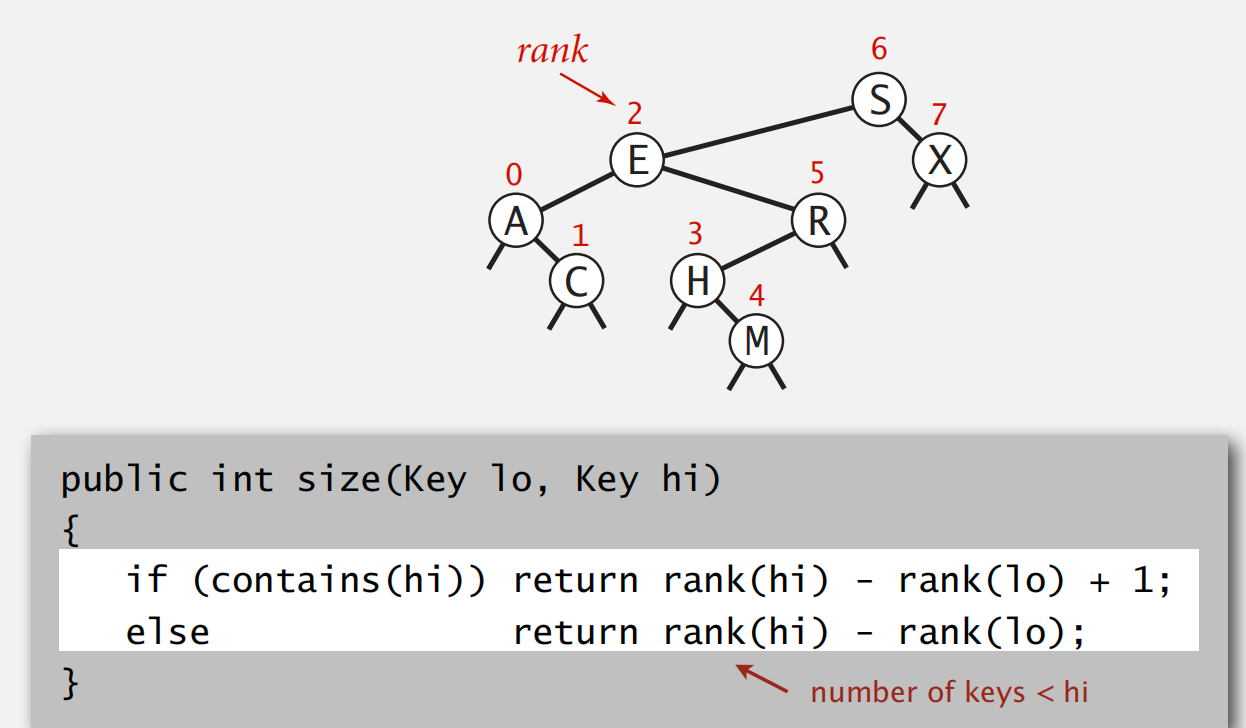
1d Range count
要求:在 logN 时间内,找到指定 key 之间在表中所包含的元素数量
转化为从树底到树根搜索指定 key 的 rank 问题
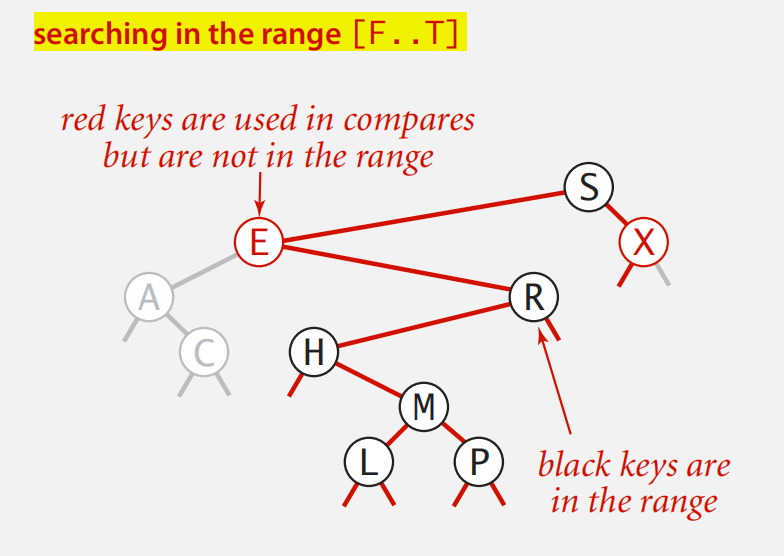
1d range search
递归搜索,遇到边界时注意判断是否左子树和右子树已不满足条件
Line Segment Intersection
扫描线算法:
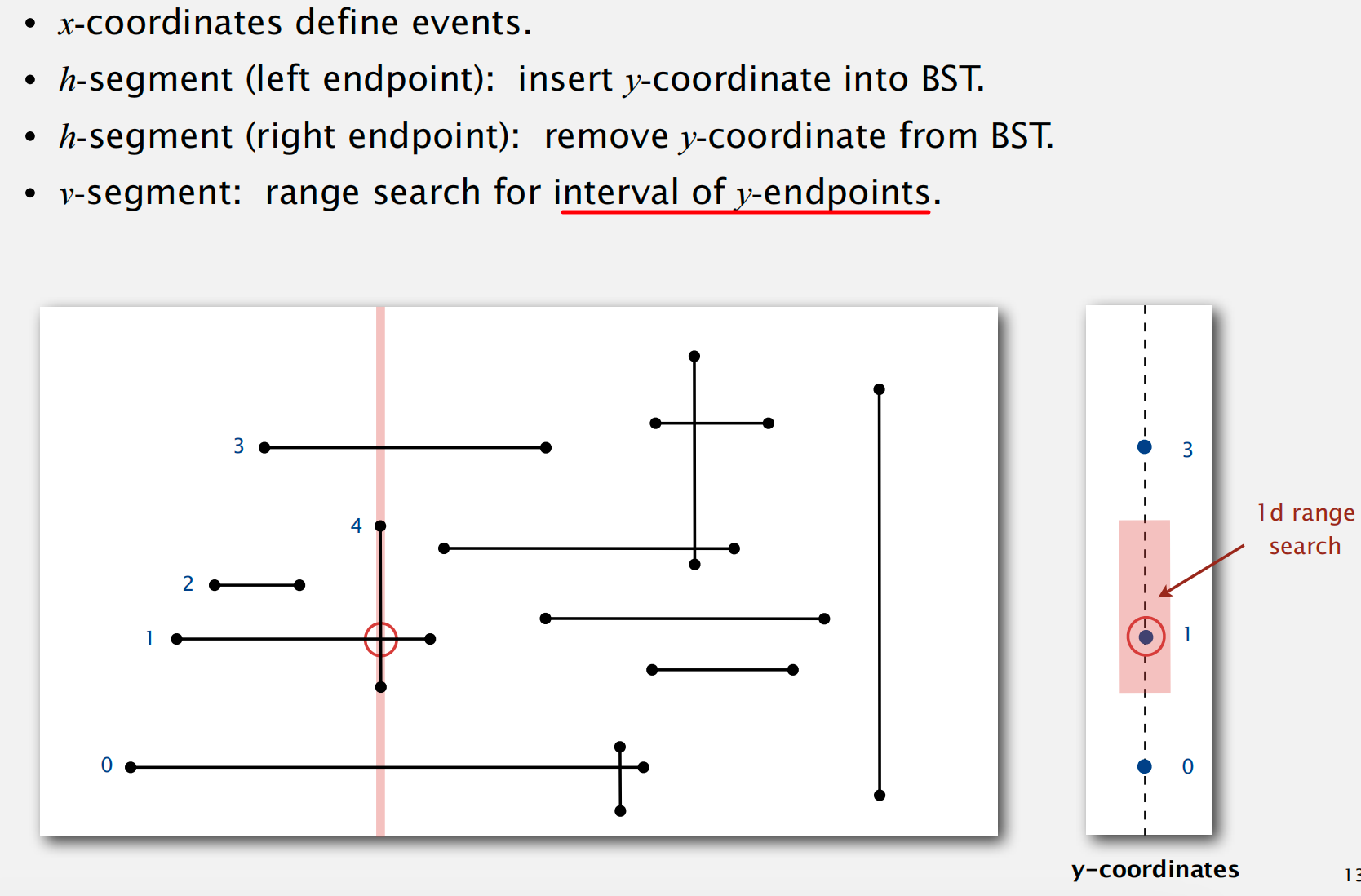
进而可以利用
logN时间的 1d range count 来实现NlogN的二维线段正交搜索算法Kd-Trees
Idea: Space-partitioning trees
利用树来递归表示二维空间的划分情况
数据机构表示
交替使用 x 和 y 坐标来表示键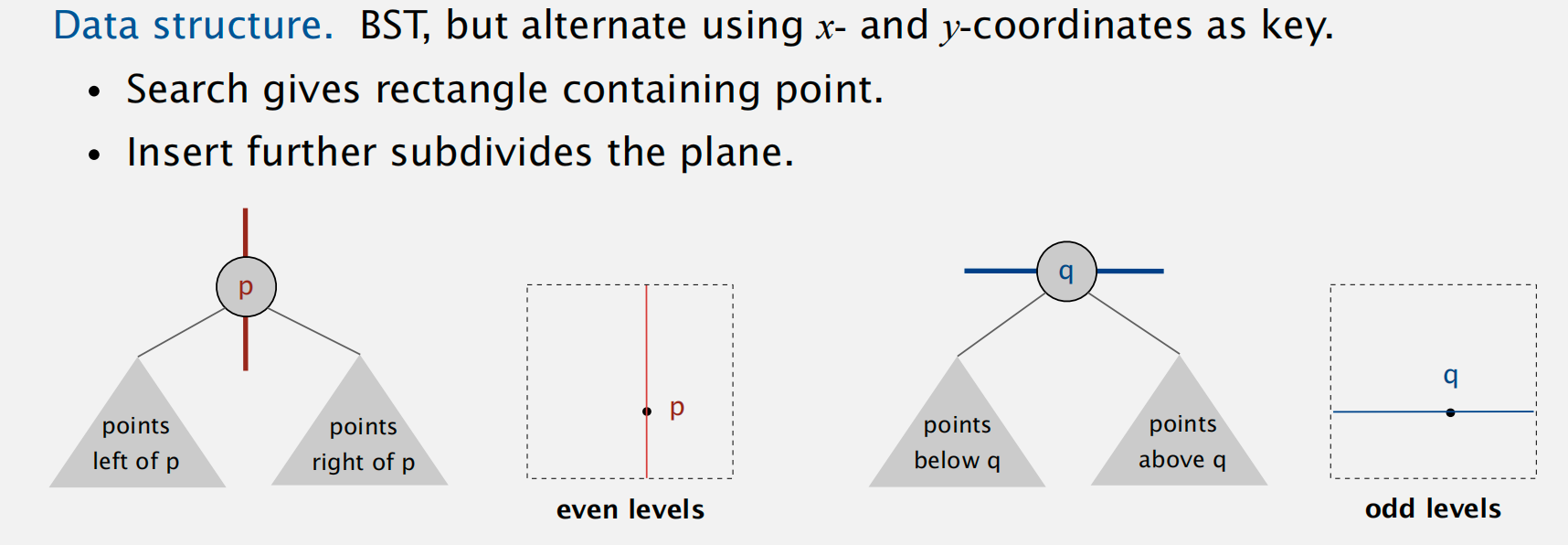
范围搜索,即指定二维区间中所包含的元素(数量)

最邻近搜索

Interval Search Trees
节点表示:所有区间的左端点
在搜索时,首先比较左子树中的最大值与指定搜索区间的左端点进行比较,如果小的话则只搜索右子树


- 如果搜索左子树没有返回值的话,则右子树中也没有交集区间存在
- 如果搜索向右子树前进的话,则左子树没有满足条件的区间
Project5: Kd-Trees
题意是通过暴力搜索和构建 kd 树的方式在二维空间搜索指定范围内的点以及最近距离的点
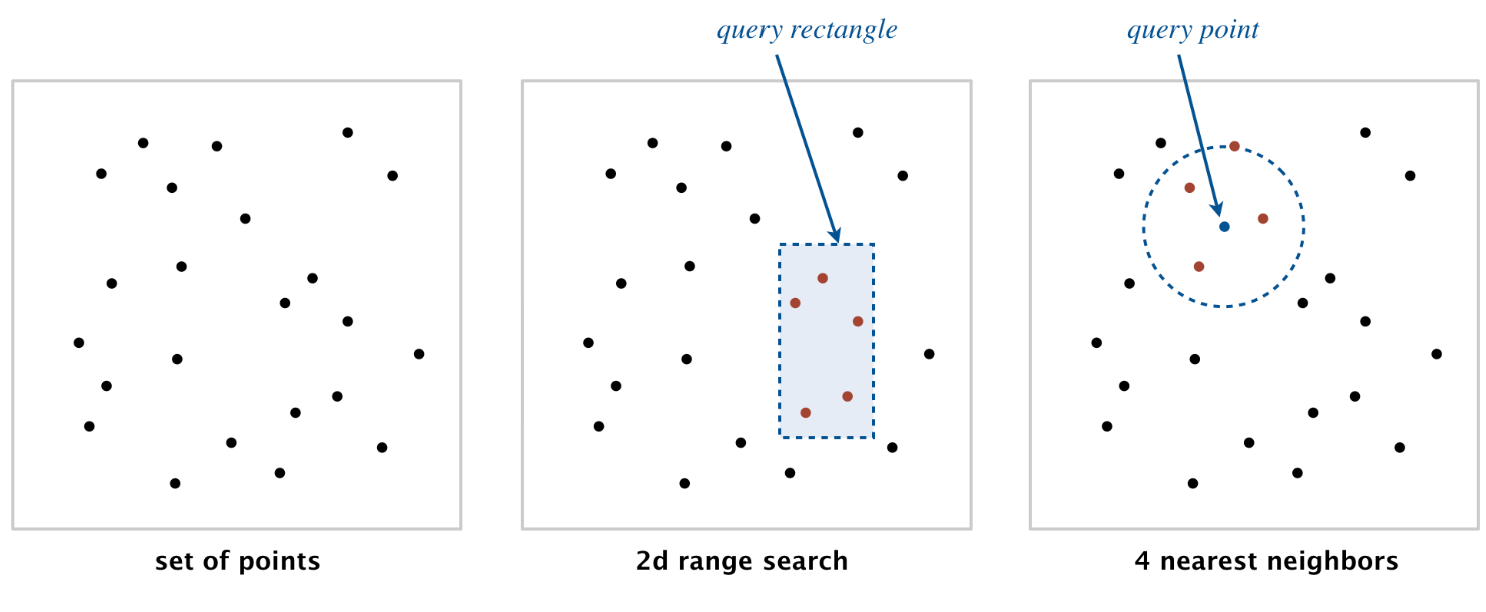
暴力搜索比较简单,可以作为后续检验 KD tree 作区间搜索算法正确性的参考,难点在于 kd-tree 树的构建,题面给出了提示可以参考 BST 相关 API 的实现
拟解决的问题
题目提示给出了 kd tree 节点的表示
1
2
3
4
5
6private static class Node {
private Point2D p; // the point
private RectHV rect; // the axis-aligned rectangle corresponding to this node
private Node lb; // the left/bottom subtree
private Node rt; // the right/top subtree
}“using the x- and y-coordinates of the points as keys in strictly alternating sequence”
如何根据当前轮次来确定下一轮空间的划分是垂直划分还是水平划分呢?
插入节点时,如何来依据父节点构建新的 rect?
- 如何画图?
- 如何作 range 搜索?
- 如何作 nearest 搜索?
解决思路:
- 我们知道 0 2 4 6 … 轮次构建新的节点时,是按照垂直划分 line, 奇数轮次水平划分,那么这样的话首先一个思路就是可以添加一个字段判断当前节点位于奇数轮次还是偶数轮次;或者直接声明当前节点划分 line 是水平的还是垂直的 (利用 enum 枚举类)
- 依照前一问题得到的水平线,我们可以进一步添加方法
nextSpnextLBnextRT来利用父节点找寻下一节点水平线的方向以及 rect 的坐标,在插入新节点的时候便可以依次构建 根据题意:“all the points to the left of the root go in the left subtree; all those to the right go in the right subtree; and so forth, recursively”。首先根据当前节点的水平线方向以及 rect 的区间范围 + point 的坐标来画出分割线,然后参考先序遍历,先画当前 point,然后一次便利左子树和右子树。

“if the query rectangle does not intersect the rectangle corresponding to a node, there is no need to explore that node (or its subtrees)”
这一点对于优化很重要,只有当前 rect 与目标 rect 存在交集才会进一步遍历,否则没有必要,作剪枝处理。实际实现时分三种情况处理:
- 当前 point 正包含在指定 rect 中,那么左右子树的 rect 也一定与指定 rect 存在交集,继续遍历两边节点即可
- 若当前 point 不包含在指定 rect 中,那么就需要判断左子树以及右子树中哪一边有与指定 rect 交集的:
- 左子树中的 rect 有存在交集的:
rect.xmin < node.p.x - 右子树中的 rect 有存在交集的:
!(rect.xmax < node.p.x)
- 左子树中的 rect 有存在交集的:
“if the closest point discovered so far is closer than the distance between the query point and the rectangle corresponding to a node, there is no need to explore that node (or its subtrees)”
首先要去判断当前最近点距离同目标点与当前搜索点所在矩阵的距离哪个更小,如果前者更小,则当前遍历点及其子树中一定不存在更近的点;进一步按照这个比较思路,往往与目标点同侧的子树更容易出现最近点,所以每次优先同侧子树进行遍历 “you always choose the subtree that is on the same side of the splitting line”
那么如何判断目标点在当前点的哪一侧呢,可以通过坐标直接判断

Ch5 Undirected Graphs
DFS
key thing: not going anyway twice
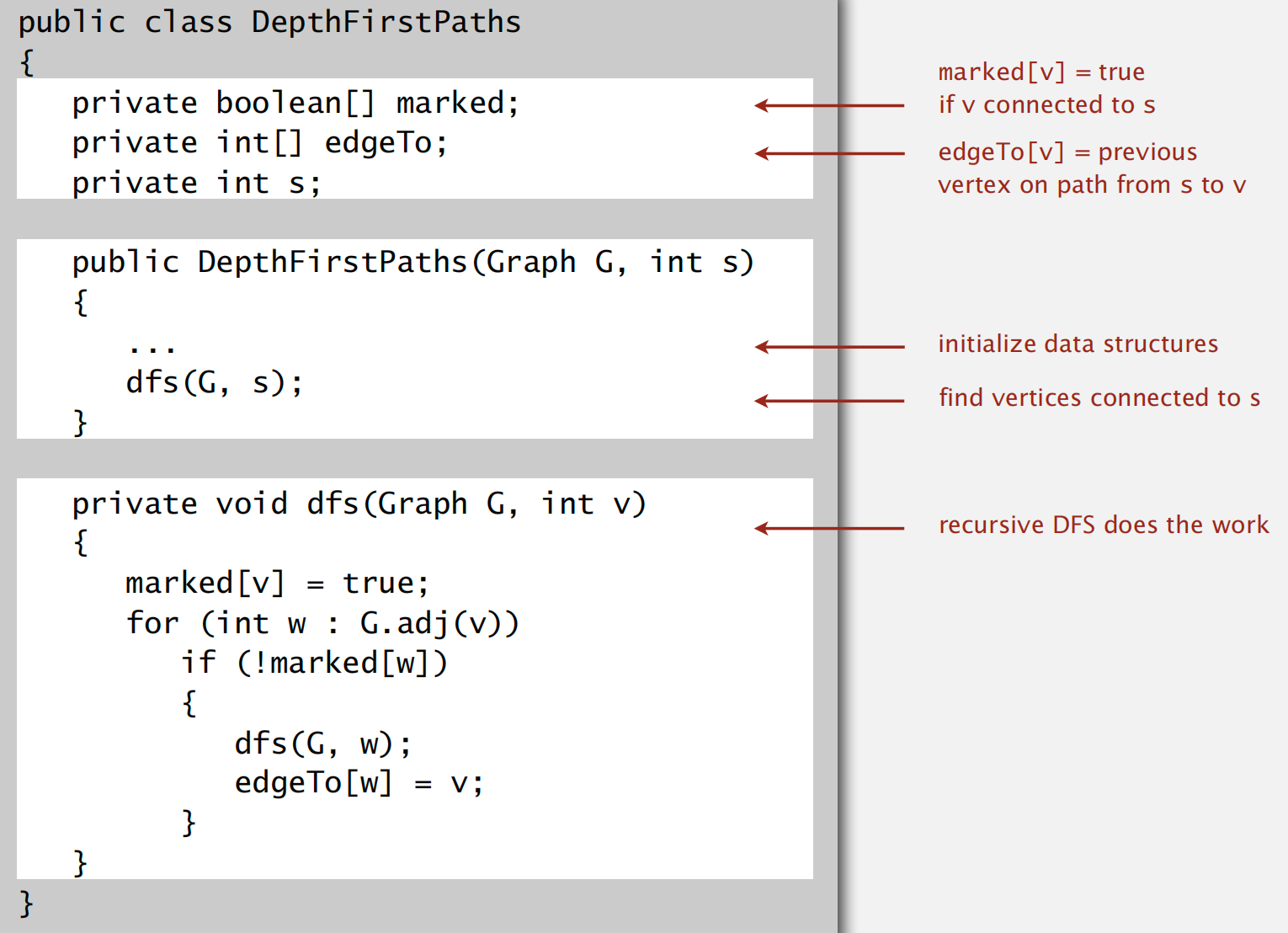
API: 将图数据结构解耦,抽离出一个寻找路径的图处理接口,方便客户端查询相关信息

DFS 算法流程以及所需的数据结构

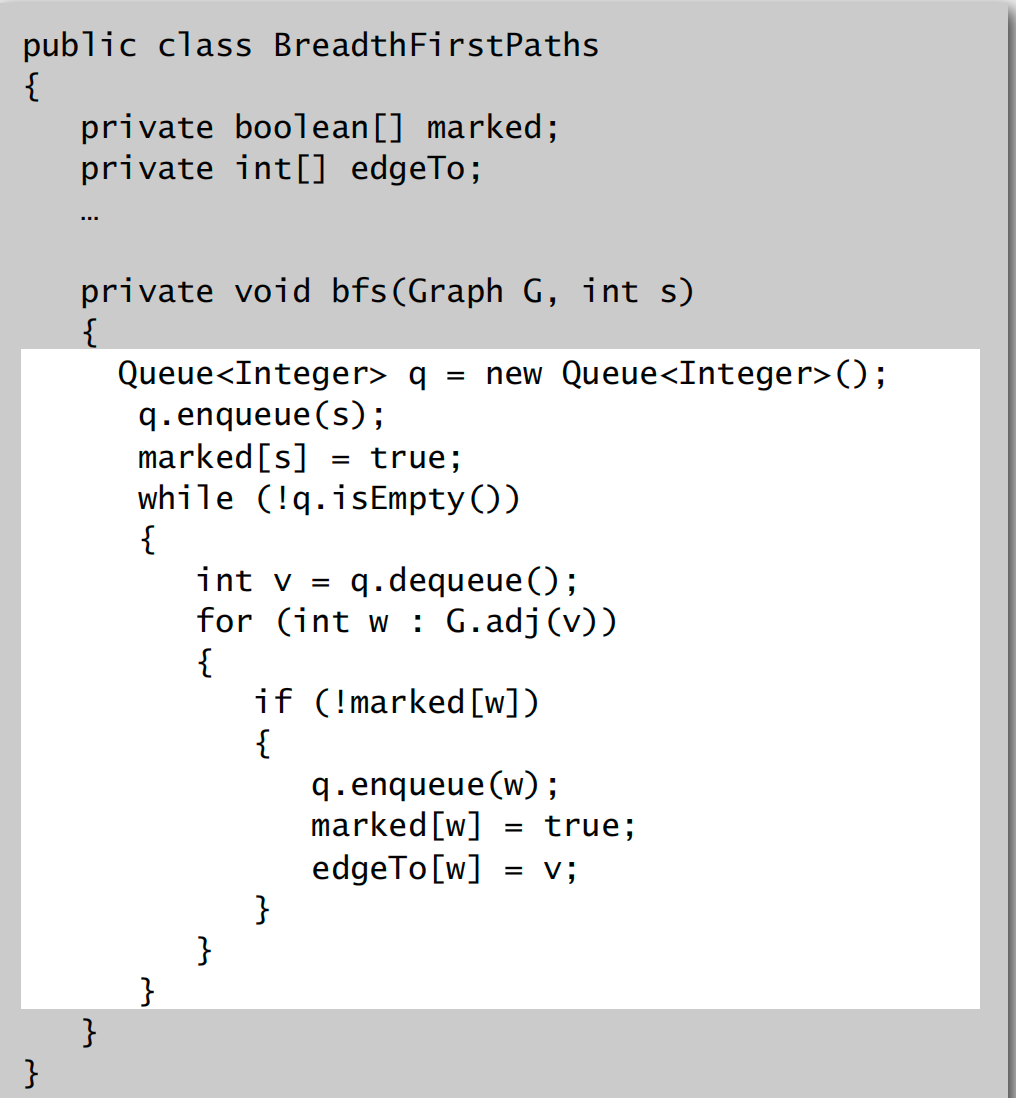
BFS
代码实现
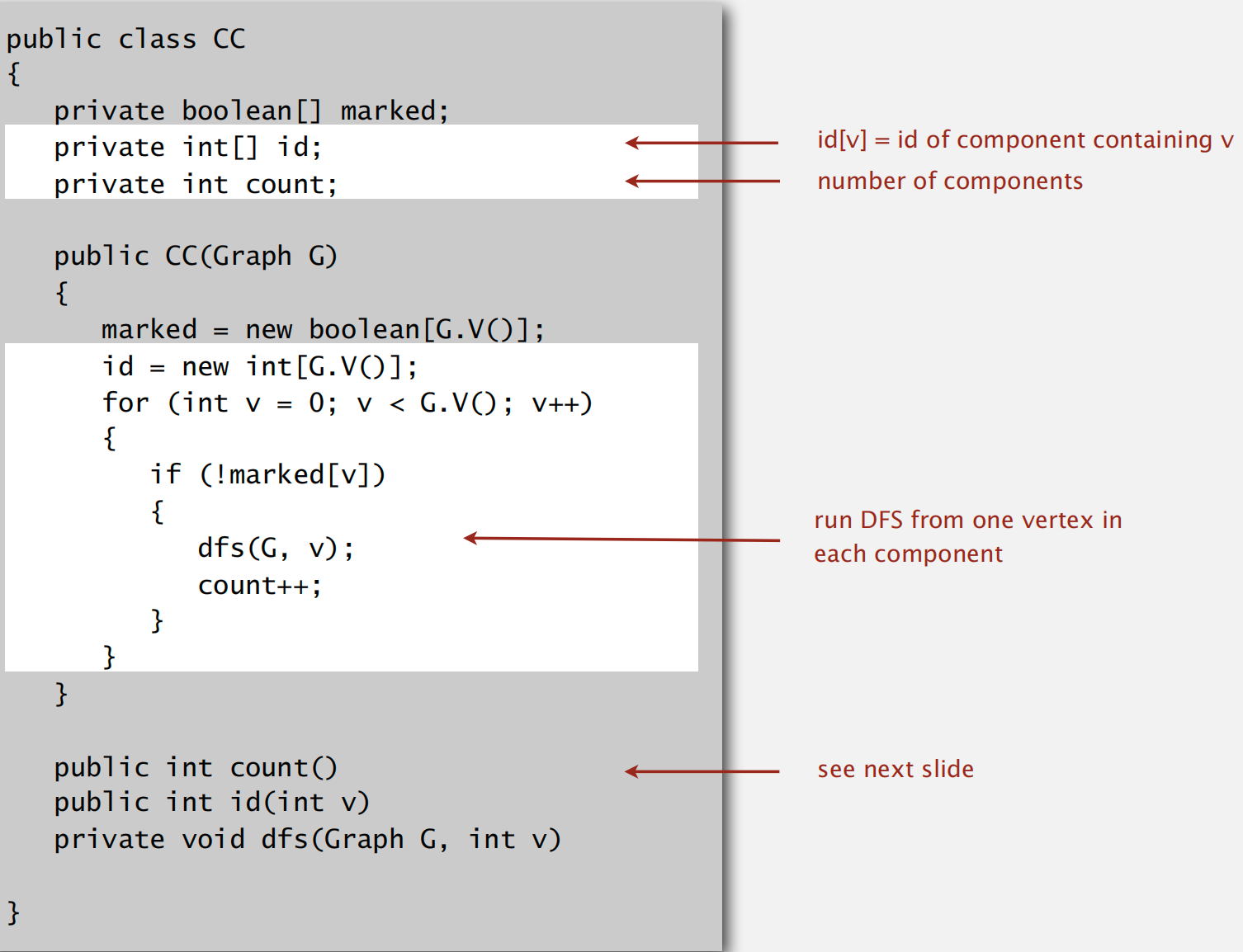
Connected Components
目标:经过预处理之后,可以在常数时间内快速判断两个节点之间的连通性
idea: 利用 DFS 搜索节点,同时做好 mark 以及记录所有联通的节点

Challenges
- 二分图问题
- 图环路问题
- 欧拉回路
- 汉密尔顿回路
- 图相似性问题
有向图相关
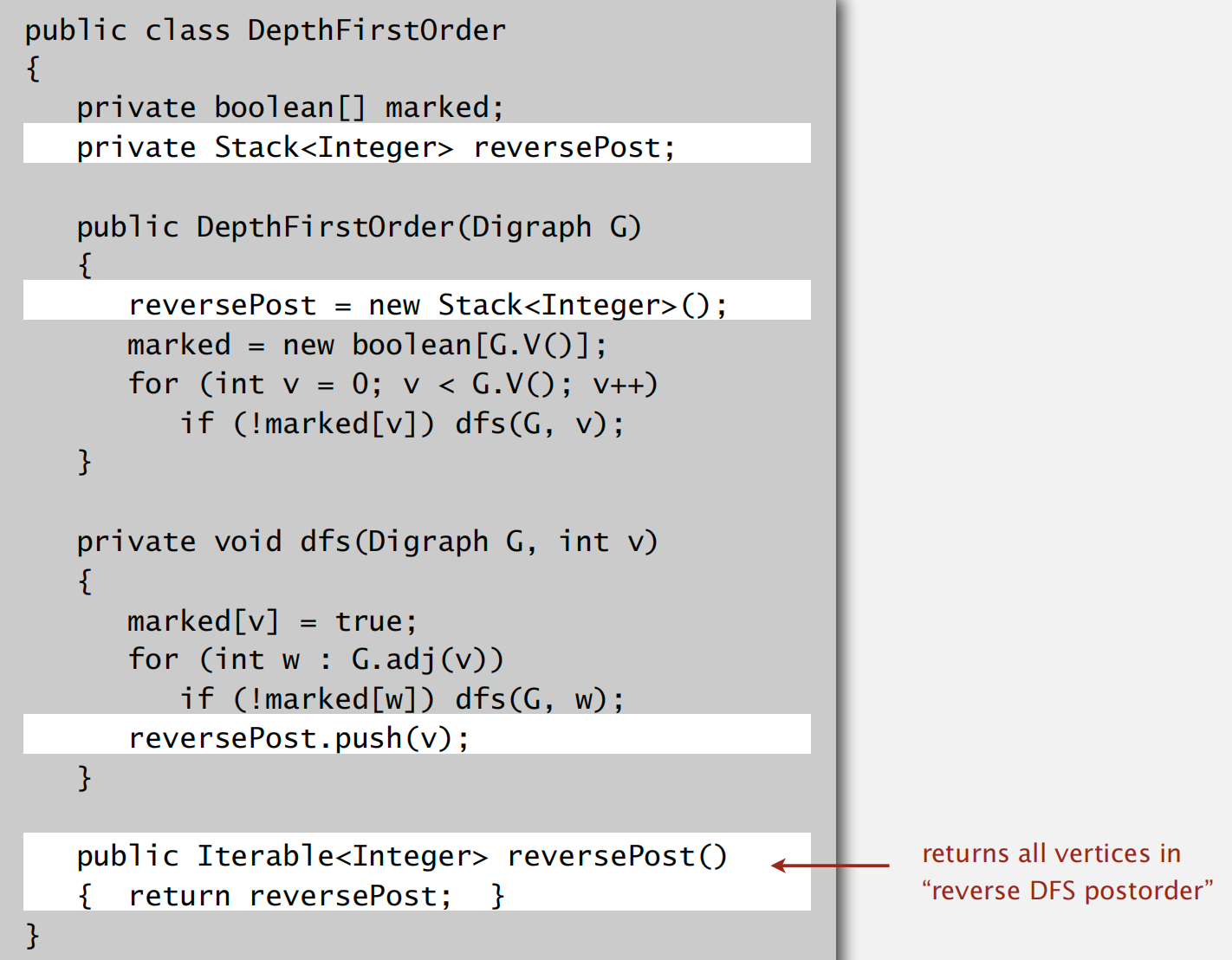
以 DFS 的方式进行拓扑排序
只需要在深度遍历的基础上维护一个栈结构保存访问顺序即可
强连通子图构造
「Kernel DAG」:

整体思路:首先做一遍拓扑排序,然后整理保存逆序结果;接着按照逆序的顺序做类似无向图的 DFS 遍历,将所有可达的元素标记为相同的序号,直至所有元素均遍历一遍
Project6: WordNet
题面
建立同义词集作为节点元素的类树结构(有向无环有跟图,但是根似乎不重要),边集反应同义词之间概念大小的关系,我们可以在图上通过计算最短距离、最短公共祖先来衡量同义词之间的相对距离关系
难点以及 trick
这次总算体会到了一些输出测试的 idea,以及如何构建数据结构,以及在其上搭积木综合运用。一开始上来从 wordNet 开始做直接懵了,有很多复杂的数据结构(映射)不知道怎么构建起来的,但是如果按照 tips 做的话实际是水到渠成的。
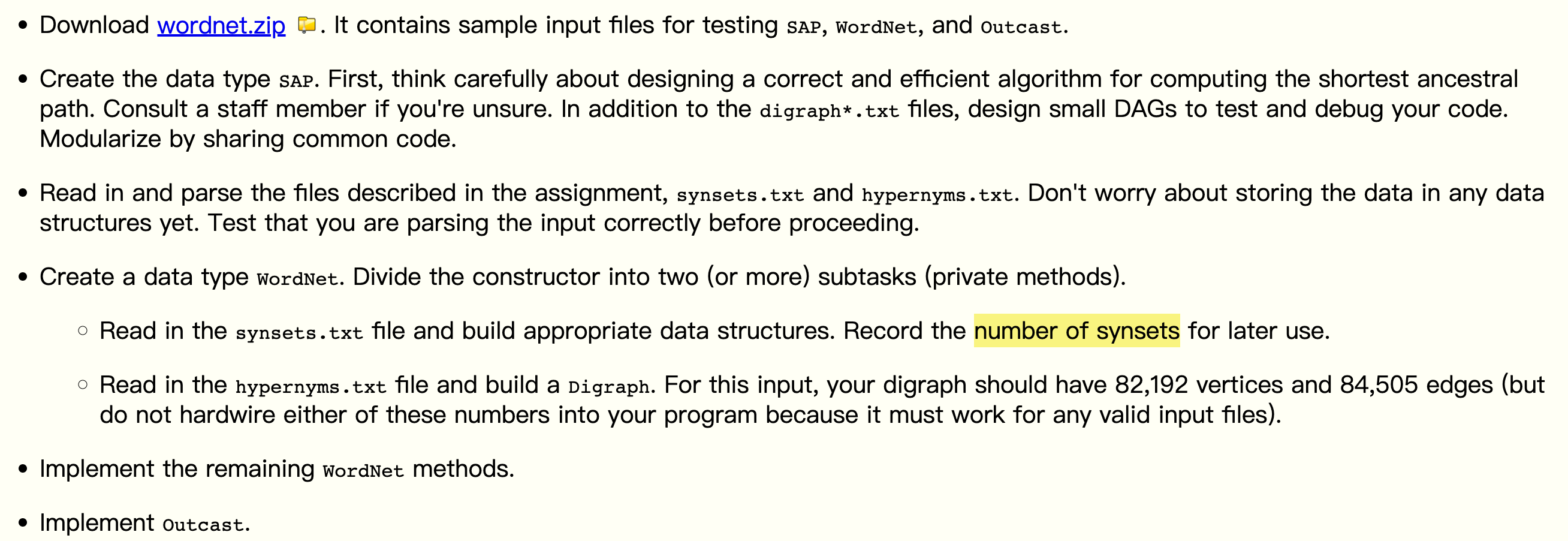
从 SAP 开始编写代码,图的建立后面再说,第一个需要解决的问题是如何计算两点之间的最短距离,课程为我们提供了 BFS 的实现,偷懒一点就直接调用即可。对于最短公共祖先的计算,相对暴力的方式就是枚举图中所有节点,分别计算目标两点到其之间的距离之和,距离最短的对应的枚举点就是最短公共祖先,对应的距离就是最短距离(当然也需要考虑不可达的情况)
对于点集的情况,BFS 的实现中也考虑到了多源最短路径计算
这里我们可以发现调用时传递的参数都是 int 类型,但是在 WordNet 中的
distanceAPI 是传入的字符串参数,因此接下来写 WordNet 的时候,首先需要维护一个单词字符串到对应整数编号的映射,考虑到单词可能出现在多个集合当中,因此使用Map<String,Set<Integer>>来实现;同理,这里返回值也需要返回synset数据集当中的第二字段,因此还需要 ArrayList 来维护数据(下标对应编号)。同时根据 tips 中给出的测试结果,我们还要记录所有单词的数量(即synset数据集当中第二字段存在空格分隔,进一步拆分)弄清需要维护的数据结构,后面就按照对应的字段从文件中按照格式读取即可,灵活使用
readLine()split()Integer.parseInt()来处理数据

Ch6 Minimum Spanning Trees
greedy algorithm
利用到的一个关键性质: Cut Property
反证法证明:
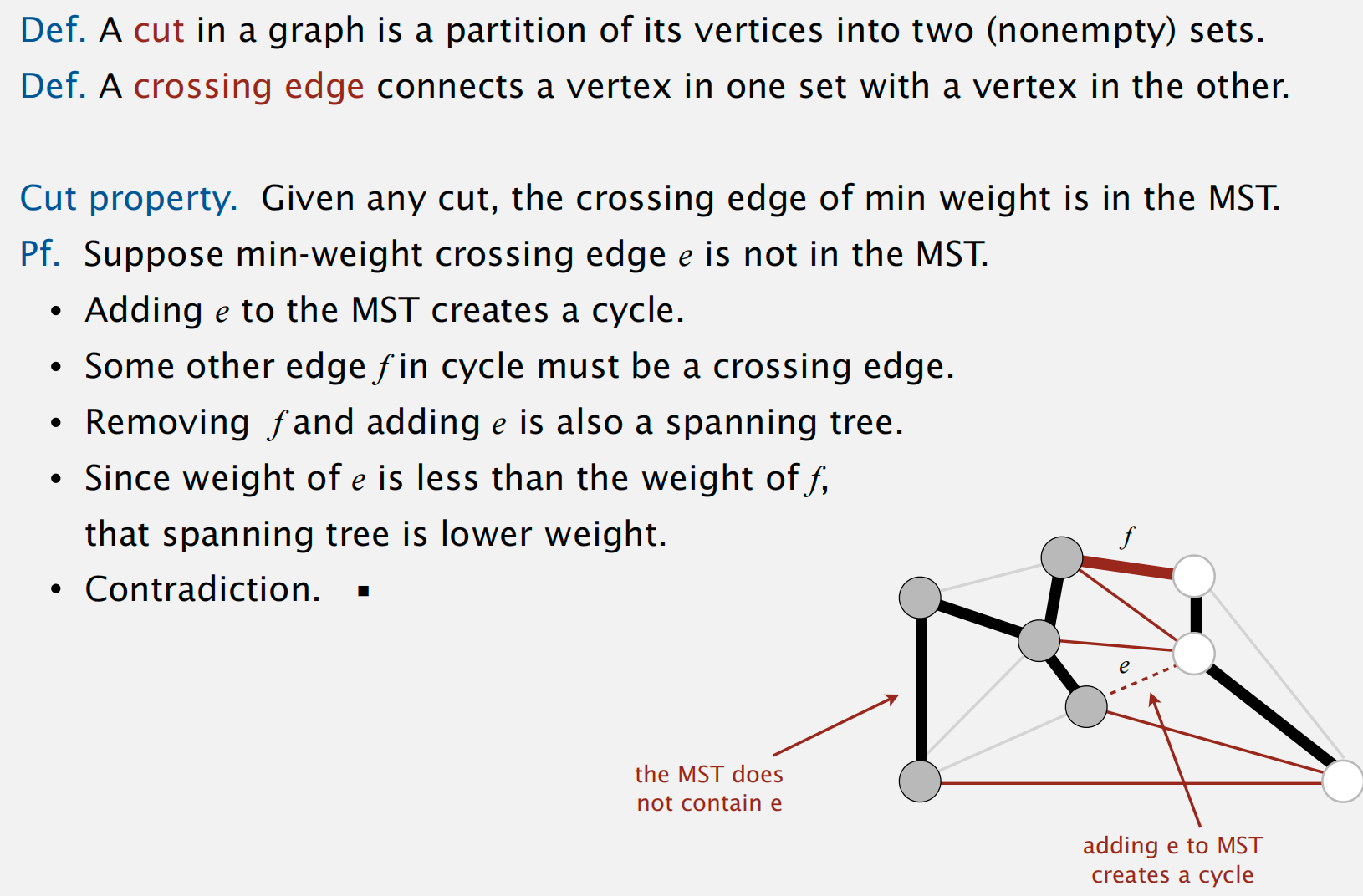
利用 greedy algorithm 可生成 MST

如何实现?
需要解决的问题:
- how to choose the cut?
how to find the minimum weight edge in the cut?
Kruskal’s Algorithm
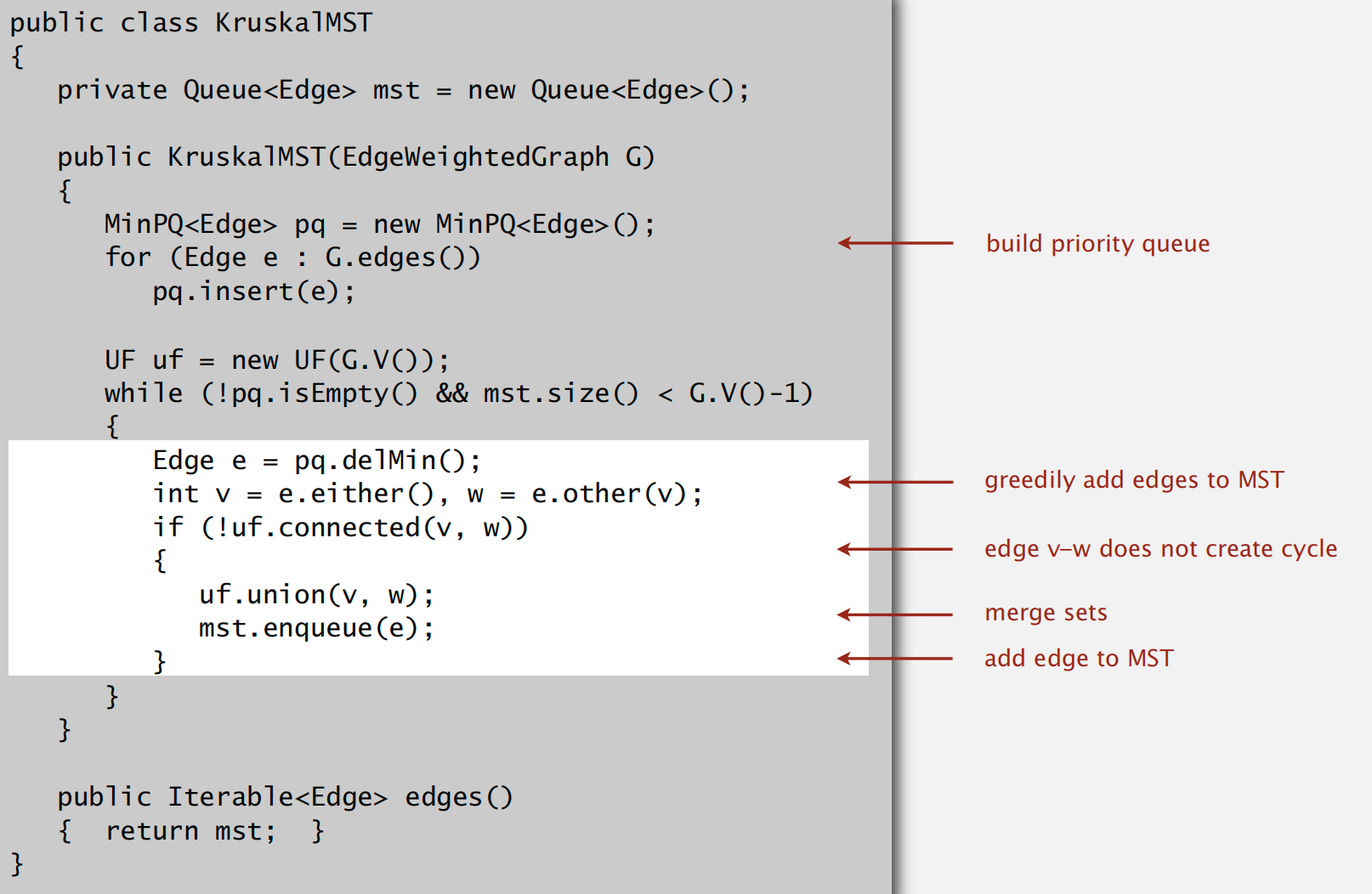
running time: ElogE
Prim’s Algorithm
算法流程:

实现有多种:
lazy implementation

总体上思想就是每次选择不在 MST 上的点和在 MST 上点构成边的最小值,将该端点加入 MST,并将其不再 MST 上的邻边点也加入到优先级队列当中,在出队入队过程中,可能以前加入的边已经变成两端点都在 MST 中的情况,这时忽略即可,更新直至 V - 1 条边
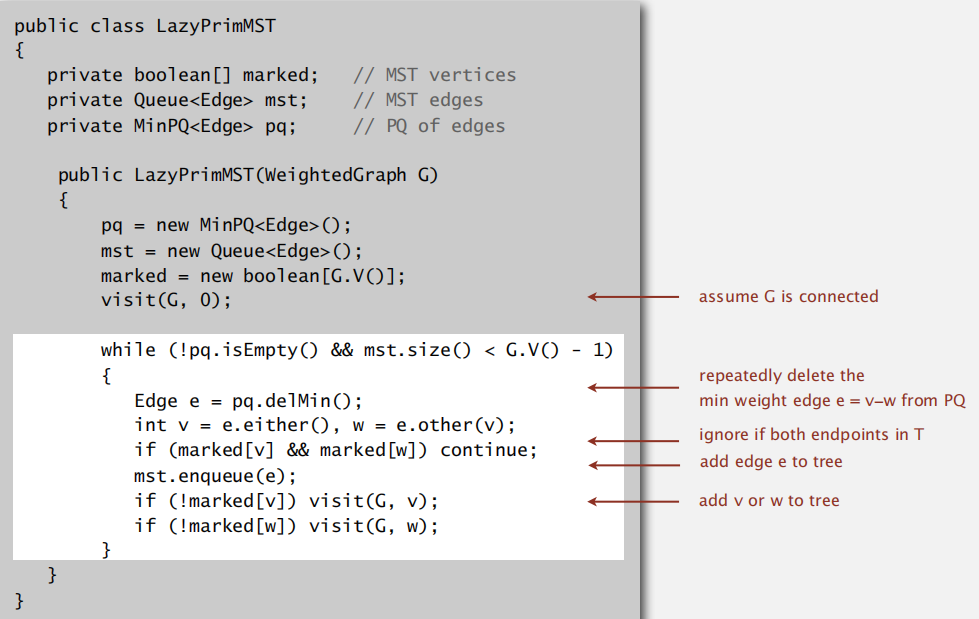

注:放入优先级队列当中的 Edge,每个元素至少有一个端点位于 MST 中
Running time: ElogE
eager implementation
也就是优先级队列不再出现冗余的边,而维护的是点到 MST 的最短距离

Shortest Paths
shortest-paths properties
最短路径的终止条件:

计算最短生成树的通用算法模型:

Dijkstra’s Algorithm

implementation
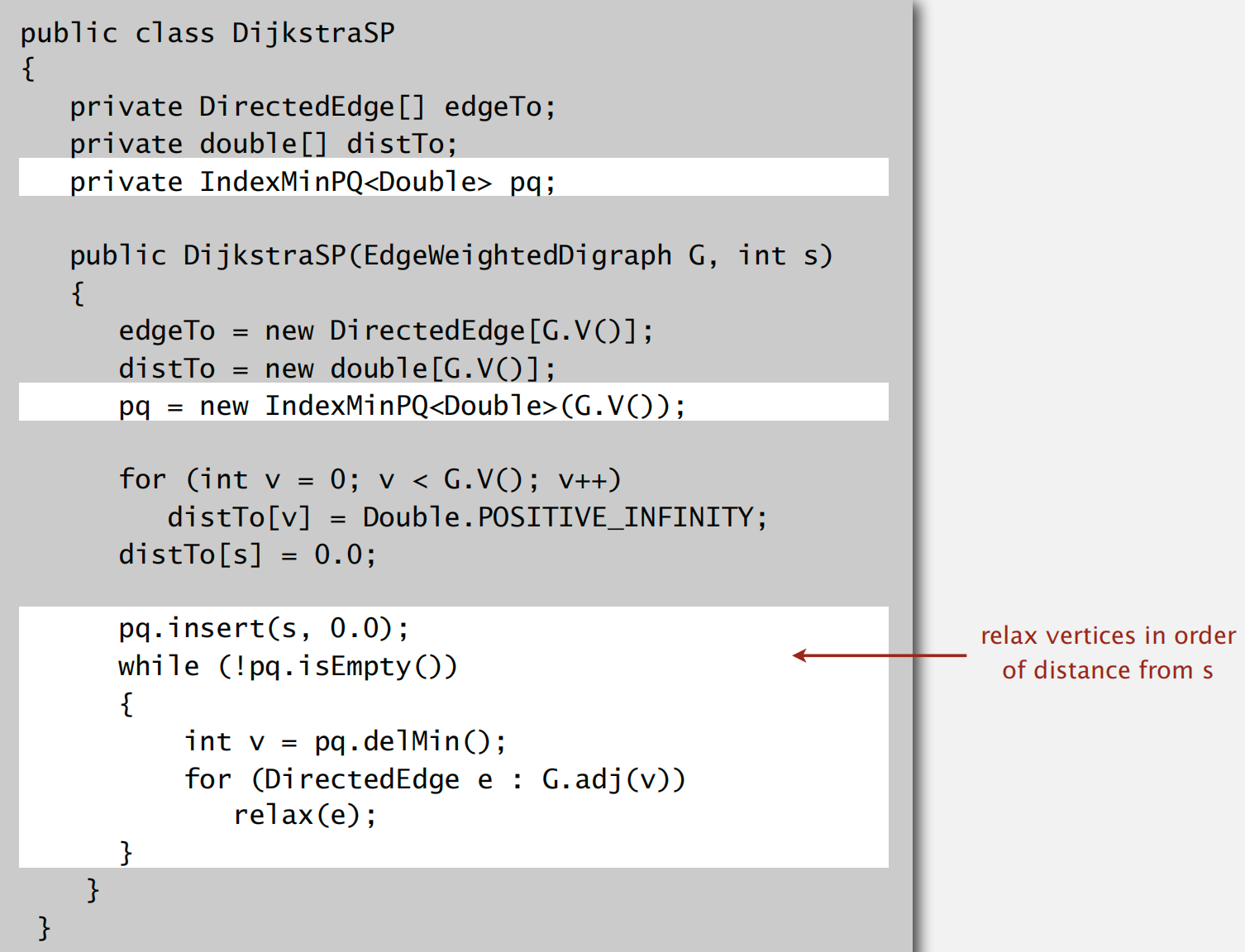

Edge-Weighted DAGs
另一种最短路径算法:先做一遍拓扑排序,再按照拓扑顺序访问节点并 relax 所有邻边;拓扑排序可以保证即使出现负权边依然可以更新 edge 至停止
Negative Weights
Bellman-Ford Algorithm 前提:无负环(但可以处理正环)
进一步优化:观察到如果 distTo[v] 在第 i 轮未更新的话,则第 i + 1 轮也无需考虑所有 v 的邻边
如何来找以及记录负环?
观察到负环会导致边的更新出现死循环(Bellman-Ford)
Project7 Seam-carving
题面
菜得抠脚。。。写代码还是一坨答辩,很难整理出一个比较好的结构模块,方便在各个地方调用。这道题是利用图的最短路径算法来处理图像高质量放缩问题,对于每一像素点,都可以利用 dual-gradient energy 公式计算得到一个权重,通过最短路径搜索算法来找到一个自上至下(自左至右)最小权重和路径,去除之后仍然能得到一个高质量的防缩图。
拟解决的问题
问题实际上真的多的一,如果数据结构涉及好,对于二维数组的处理一顿双层遍历,真的就是时间加空间全都爆炸,自己写的也就能过50分。。
参考某不知名大神的代码:https://github.com/KarahanS/Coursera-Princeton-Algorithm-II-Projects/
- 对于每个像素点,计算得到的权重如何处置?题面给了提示(“you can save the energies in a local variable
energy[][]and access the information directly from the 2D array”) - 有了权重值,那么就可以做最短路径算法了,题目建议的是利用拓扑排序 + relax vertical 的方式,注意到这里的权重不在是边上,而是直接在节点上,并且每个节点都向下分叉三个边(也就是似乎按层遍历的话就已构成了拓扑排序),如何做最短路径搜索,同时还能记录下来路径序列?(题目也给了提示,构建额外的局部数据结构:“the
distTo[][]andedgeTo[][]arrays should be local variables, not instance variables” - 垂直方向的最短路径序列已出,如何处理水平方向的?题目给出了提示是先将原图像得到的信息二维数组进行转置,然后利用垂直方向的求解之后,再转置回来。由于转置需要双层遍历信息二维数组,如果多次求解水平方向的序列则会多次转置,怎么减少时间的消耗?(“if you perform a sequence of 50 consecutive horizontal seam removals, you should need only two transposes (not 100).”, “until you need to do so”)
- 有了最短路径序列 seam,如何进行 remove 操作,题目说明了可以通过
System.arraycopy()来复制原来的信息数组到新的copy中,这时还需要重新更新 energy 的权重值,但是为了节省时间,我们只需要更新沿着 seam 两侧的节点权重即可,其余都未收到影响,这里如何处理?
- 对于每个像素点,计算得到的权重如何处置?题面给了提示(“you can save the energies in a local variable
解决思路:
- 图片为了方便返回,我们预设 RGB 数组和 energy 数组来保存信息,以后对图片信息的修改和访问就通过这两个数组即可实现。在调用 picture() 方法时创建新图片并按照信息数组中的内容赋予相应值即可
我们按照公式以及给定的坐标计算好 energy 将其存储到实例变量数组当中即可,需要的时候直接取即可,这里有个细节问题在于,我们再在测试客户端代码以及 energy 的注释上都可以发现,参数的顺序是先 col 后 row,需要注意访问数组时的下标顺序。
1
2
3
4// energy of pixel at column x and row y
public double energy(int x, int y) { // col x row y
//////
StdOut.printf("%9.2f ", sc.energy(col, row));这里为了方便我们单独抽离一个 API
computeEnergy专门用于计算能量权重(这时下标顺序与存储顺序一致)这里遗留一个 bug 需要特别注意,就是在判断边界的时候,如果按照当前 energy 边界来计算的话会出错,因为我们在去除 seam 更新 energy 数组时边界是会 -1 的,因此不能用更新之前的 energy 数组作边界判定
1
2
3
4// 这里如果仍调用会出错
if (x == 0 || y == 0 || x == RGB.length - 1 || y == RGB[0].length - 1) {
return BORDER_ENERGY; // 1000.0
}对于最短路径的搜索,我们直接按行枚举,保存好对于每一个节点其 distTo 和 edgeTo 的状态值(对于第一行,distTo 就是其本身,edgeTo 设置为无效值);每一个值由于可以拓扑序列到向下的三个节点,因此逐一判断由当前节点向下是否会使得对应点的 distTo 减小,如果可以则更新。最终在最后一行通过枚举即可找到由上至下权重和的最小值,并通过 edgeTo 反向搜索找到这条路径
- 首先对于转置,我们需要新创建 RGB和 energy 数组并存储原数组转置之后的值,并更新。如果频繁调用的话一定会导致时间复杂度上去。为了解决该问题,我们应该在需要的时候才转置,什么是需要的时候?即当需要处理水平方向的最短路径问题,而我们处于垂直方向状态时(或者需要处理垂直方向而当前处于水平方向的时候),才会去调用 transpose 转置方法。为此,我们设置一个全局布尔值来表示当前是处于水平状态还是垂直状态,这样当找寻路径以及后续移除路径时,先去判断方向是否正确再去完成任务。(这样重复任务时就不需要频繁的转置)
- 对于 remove seam 操作,也是用
System.arraycopy()来复制原 RGB 和 energy 到新的宽度x高度数组中去,RGB 直接更新即可(并且后面 energy 更新时需要用到);energy 再更新后还需要更新 seam 两侧的能量权重值,当然这里需要特殊判断一下 seam 所在列是否处于左边界和右边界
Ch7 Maximum Flow and Minimum Cut
图片失效
PS: 图片好像失效了,详见课程 slides
Mincut problem
最大流问题
st-流需要满足两个性质,基于流引出最大流问题
Ford–Fulkerson Algorithm
运行模式:参数化路径,存在正向和反向两种边,为了保证 equilibrium 性质
终止条件:
- 空值反向边
全值正向边
The algorithm is to find all of the vertices reachable from s using only forward edges that aren’t full or backwards edges that aren’t empty
==相关理论定理及证明:==
Flow-value lemma
weak duality
Maxflow-mincut theorem
Java Implementation
构建 residual network,方便 argumenting 时选择 forward edge/ backward edge
Augmenting path in original network is equivalent to directed path in residual network
Project8 Baseball Elimination
- 题意:利用最大流算法来解决体育竞技当中冠军排除问题
- 思路:整体难度不高,均有封装完善的数据结构API可供使用,整体从读入文件开始,分别设置到对应的数据存储数组当中,适当构建队伍名称到下标的索引映射;按照平凡和非平方情况分别求解给定队伍是否会被排除,对于非平凡情况,需要构建网络图,按照指定结构构建,并作最大流计算。注意是否仍有剩余的比赛未比完该如何判断呢?结合最大流的判定可知,只需判定当前是否仍存在 augmentingPath 即可
STRING SORTS
Alphabets
Key-Indexed Counting
前提条件:keys 需要携带关联数据信息
算法流程与实现:
(假设 a~f 代表 0~6)
时空复杂度 O(N+R); 具有稳定性
LSD Radix Sort
证明这种排序方法使得固定长度的字符串呈升序:
前提:Key-Indexed Counting 排序操作具有稳定性
MSD Radix Sort
与 LSD Radix Sort 类似,只不过比较顺序是从 left 到 right
递归的实现方式:注意到 counter 数组不可以重复使用,但是 aux 可以
优缺点:递归过程空间复杂度爆炸;
3-way string quicksort
quick sort 与 MSD 的结合
Suffix Arrays
Idea:
整理出数组的所有后缀子串,并作排序,可以将重复的序列值靠近
Ch8 Tries
R-way tries
R 取决于 Radix 大小
how to search in tries?
Ternary Search Tries
PS: 注意 deep 的变化
Character-Based Operations
support operation:
- Prefix match
- WildCard match
Longest prefix
==「Warm up」==:采用先序遍历访问并添加 Tries 上的所有 String key(包括所有 prefix) 到 queue 中
==「Prefix match」==:直接先找到前缀节点,然后调用 collect API 即可
==「Longest prefix」==:记录最后一次匹配到的 string key 即可
Substring Search
朴素做法
backup version
Knuth–Morris–Pratt
intuition: 我们已知模式串的前缀了,因此在匹配主串时需要充分利用这个信息
基于有限状态机的实现:其中一维表示匹配主串的字符,二维j代表当前状态
可以看到这里 i 是不会自减的,时间复杂度 O(n)
如何构建 DFA?
如何 maintain state X ?
时间复杂度 O(RM) (R 指 radix)
Boyer–Moore
基本思路
跳过多少字符呢?
如果主串 mismatch 的字符未出现在 pattern 中,则直接跳过改字符;
否则匹配 pattern 中最右侧的对应字符
时间复杂度:O(M/N) (最坏情况,第一个字符均匹配失败,O(MN))
Rabin–Karp
basic idea
如何有限次计算 hash 并快速 search pattern ?
线性计算 hash:
Xi 之间计算 hash:
search ⇒ Monte Carlo version
该版本的 search 可以保证速度,但不能保证准确性,因为随机素数 Q 易出现碰撞;
Project9: Boggle
参考:Princeton Algorithms, Boggle – 凝神长老和他的朋友们 (jxtxzzw.com)
题面比较易懂,在一个 4x4 的格子上可以上下左右+对角线6个方向作 dfs,并判断得到的单词序列是否位于字典当中,讲得到的单词按照长度进行量化分数并输出最终的总和
拟解决的问题
题目思路乍一看非常好求,直接暴力 dfs 拿到所有可能的单词及其前缀,然后判断是否位于字典中即可,但是随着数据量增大,时间复杂度如果不对 dfs 作减枝处理势必会很高。
主要影响时间效率的几大问题:
dfs 如何作减枝,tips 中说明了可以在 dfs 过程得到的字符序列作为前缀,预先判断是否是字典中某个单词的前缀,如果不是则没必要继续 dfs
刚开始我直接使用 alsg4 自带的 trie 字典树进行操作,其判断前缀的方式通过递归处理,一定程度上效率较低,同时每 dfs 一层实际上字符序列仅仅多加了一位,但是频繁进行前缀判断,时间复杂度并未有效降低
另一个主要影响因素在于 dfs 过程中,无论是通过 String 还是 StringBuilder 来记录路径上的字符,都极大的影响时间性能
解决思路:
充分深入运用字典树的特性
对于第一个问题,首先我们是可以递归处理该换成循环处理的,在构建存储字典中单词的数据结构时,就将其插入到字典树当中,并在尾节点处设置单词字面量值,其余中间节点的字面量值为 null;
另外,对于频繁判断前缀的问题,我们已经有了一个 Observation:dfs 每次只会更新1位字符,因此我们可以维护一个 cache,表示上一层 dfs 字典树节点的状态,这样判断是否会前缀只需简单的 if 判断:
1
2
3
4
5
6if (cache.contains(c)) {
// prefix is true, update the cache to the current dfs node
cache = cache.get(c);
} else {
cache = null;
}因为 String 操作上带来的时间影响,因此我们可以将所有的字面值预先存储在字典树中,当 dfs 完整达到尾节点时,就可以直接拿到对应的值。
这里题目有个特殊的 case 在于,u 字符总是紧随 Q 字符之后,因此所有字典当中不符合这种特征的单词都可以直接忽略,因为 board 中不会产生,少去了一部分探索 Trie 时间消耗
Ch9 Regular Expressions
概念
符号表示一组字符串集合(集合可以是无限的)
REs and NFAs
==「NFA」==规则
NFA 模拟:
基本 idea
已维护的 i 符号读后的状态,经过读入第 i+1 个符号后的状态转移 + null 转移后得到的状态,成为 i+1 符号读后的总状态
对于给定状态集合,获取其所有可转移到的状态,可以通过图深搜可达性实现
Java Implementation
最坏时间复杂度: O(MN)
构建 NFA
从基本操作模块开始,包括:闭包、或操作
因此需要通过 stack 来维护符号
(和|,遇到)时弹出并构建上述基础操作模块的 NFA
Data Compression
哈夫曼编码
前提:要求编码是自由前缀的,即任何一个字符的编码不能是其他字符编码的前缀,避免歧义
构建表示:二进制字典树 trie
LZW
可以看到这里经常需要匹配输入序列的前缀,因此 trie 数据结构比较合适存储
expansion 操作:与压缩操作时一致,构建相同的 trie
不过构建的一个区别点在于将编码转换回字符序列的时候,仍需要记录新的字符前缀
tricky case: 会出现扩展时编码值比前缀 trie 构建先出现的情况
Project10: Burrows–Wheeler
- 题意:通过实现三个模块来构建压缩函数,这次算是独立完成了大部分的工作,虽然最后空间消耗比较大,但总体时间和正确率还不错
记录困难点
Circular suffix array 输出 sorted suffixes 最后一列的字符
这里刚开始直接调用的 sorted suffixes 字段、取出元素的指针字段并输出指向字符串的字符,但是 sorted suffixes 字段必须得是 private 修饰才行,因此这个思路不同。观察到 index 方法的作用:返回 sorted suffixes 中元素对应在 original suffixes 中的位置,可以看到 original suffixes 下标实际就对应着字符顺序,因此用 index 也可以达到上述取指针字段的效果
Burrows–Wheeler transform 方法,难点实际在于构造 next 数组部分
tips 中给出,可以参考 key-indexed counting algorithm 部分,实际上这里就是在按照字符频率进行排序,利用 key-indexed counting algorithm 即可达到 O(N+R) 的时间复杂度,并且 next 的获取可以直接一行得到
1
next[count[s.charAt(i)]] = i;